7 根号を含む関数の積分

関数 $f(x)$ に根号 $\sqrt[n]{ax+b}$ $(a\neq0)$ を含む場合の 不定積分を考える． 変数変換

$$t=\sqrt[n]{ax+b}$$ (926)

とおき置換積分法で求積する． 両辺を $n$ 乗すると

$$x = \frac{t^n-b}{a}$$ (927)

を得る．またこれより

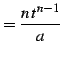$$\frac{dx}{dt} = \frac{n\,t^{n-1}}{a}$$ (928)

が成り立つ．よって $f(x)$ の不定積分は

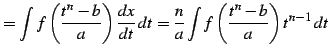$$\int f(x)\,dx = \int f\left(\frac{t^n-b}{a}\right) \frac{dx}{dt}\,dt= \frac{n}{a} \int f\left(\frac{t^n-b}{a}\right)t^{n-1}\,dt$$ (929)

より求められる．

例 6.28 (根号を含む場合の計算例)   不定積分

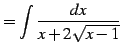$$I = \int\frac{dx}{x+2\sqrt{x-1}}$$ (930)

を考える．まず

$$t =\sqrt{x-1}$$ (931)

とおく．これより

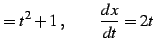$$x =t^2+1\,,\qquad \frac{dx}{dt}=2t$$ (932)

となる．よって置換積分法より

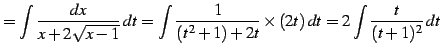$$I = \int\frac{dx}{x+2\sqrt{x-1}}\,dt= \int\frac{1}{(t^2+1)+2t}\times (2t)\,dt= 2\int\frac{t}{(t+1)^2}\,dt$$ (933)

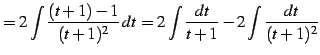$$= 2\int\frac{(t+1)-1}{(t+1)^2}\,dt= 2\int\frac{dt}{t+1}-2\int\frac{dt}{(t+1)^2}$$ (934)

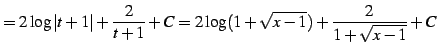$$= 2\log\vert t+1\vert+\frac{2}{t+1}+C= 2\log(1+\sqrt{x-1})+\frac{2}{1+\sqrt{x-1}}+C$$ (935)

を得る．

関数 $f(x)$ に $\sqrt{ax^2+bx+c}$ $(a>0)$ を 含む場合を考える． このときまず

$$\sqrt{ax^2+bx+c} =t-\sqrt{a}\,x$$ (936)

とおく．両辺を二乗すれば

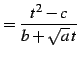$$x = \frac{t^2-c}{b+\sqrt{a}\,t}$$ (937)

を得る．これより

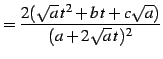$$\frac{dx}{dt} = \frac{2(\sqrt{a}\,t^2+b\,t+c\sqrt{a})}{(a+2\sqrt{a}\,t)^2}$$ (938)

となる． このとき不定積分は

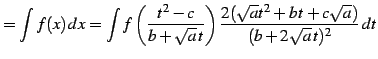$$I =\int f(x)\,dx= \int f\left(\frac{t^2-c}{b+\sqrt{a}\,t}\right) \frac{2(\sqrt{a}t^2+b\,t+c\sqrt{a})}{(b+2\sqrt{a}\,t)^2}\,dt$$ (939)

により求まる．

例 6.29 (根号を含む場合の計算例)   不定積分

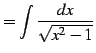$$I =\int\frac{dx}{\sqrt{x^2-1}}$$ (940)

を考える． 変数変換

$$\sqrt{x^2-1} =t-x$$ (941)

とおく．両辺を二乗すれば

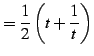$$x = \frac{1}{2} \left( t+\frac{1}{t} \right)$$ (942)

を得る．これより

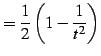$$\frac{dx}{dt} = \frac{1}{2}\left(1-\frac{1}{t^2}\right)$$ (943)

となる． よって不定積分は

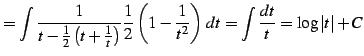$$I = \int\frac{1}{t-\frac{1}{2}\left(t+\frac{1}{t}\right)} \frac{1}{2}\left(1-\frac{1}{t^2}\right)\,dt= \int\frac{dt}{t}= \log\vert t\vert+C$$ (944)

$$=\log\left\vert x+\sqrt{x^2-1}\right\vert+C$$ (945)

と求まる．またこの結果は

$$I = \mathrm{Cosh}^{-1}x+C$$ (946)

とも表される．

Kondo Koichi
Created at 2004/08/14