Next: 14 図形の面積 Up: 6 積分法 Previous: 12 定積分と不定積分 Contents
13 定積分の計算
定理 6.43 (置換積分)
積分変数を 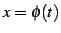 と置き換えると定積分は
と置き換えると定積分は
と表される.
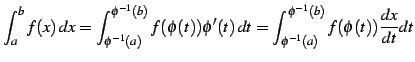 |
(987) |
と表される.
例 6.44 (置換積分の計算例)
ここで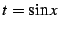 とおいた.このとき
とおいた.このとき
であることを用いた. また積分区間は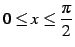 から
から
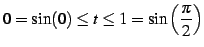 へと変わる.
へと変わる.
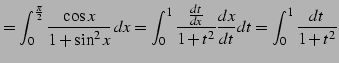 |
(988) | |
![$\displaystyle = \Big[\mathrm{Tan}^{-1} x\Big]_{0}^{1}= \mathrm{Tan}^{-1}(1)-\mathrm{Tan}^{-1}(0)= \frac{\pi}{4}-0=\frac{\pi}{4}\,.$](img2895.png) |
(989) |
ここで
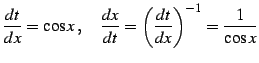 |
(990) |
であることを用いた. また積分区間は
定理 6.45 (部分積分)
![$\displaystyle \int_{a}^{b}f'(x)g(x)\,dx= \Big[f(x)g(x)\Big]_{a}^{b}- \int_{a}^{b}f(x)g'(x)\,dx\,.$](img2900.png) |
(991) |
例 6.46 (部分積分の計算例)
![$\displaystyle = \int_{0}^{\pi}x\,\sin x\,dx= \int_{0}^{\pi}x\,(-\cos x)'\,dx= \Big[-x\cos x\Big]_{0}^{\pi}- \int_{0}^{\pi}1\times(-\cos x)\,dx$](img2902.png) |
(992) | |
![$\displaystyle = \Big[-x\cos x\Big]_{0}^{\pi}+ \int_{0}^{\pi}\cos x\,dx= \Big[-x...
...Big]_{0}^{\pi}+ \Big[\sin x\Big]_{0}^{\pi}= \Big[-x\cos x+\sin x\Big]_{0}^{\pi}$](img2903.png) |
(993) | |
| (994) |
定理 6.47 (偶関数,奇関数の定積分)
関数  が偶関数のとき
が偶関数のとき
関数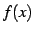 が奇関数のとき
が奇関数のとき
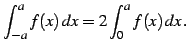 |
(995) |
関数
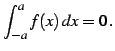 |
(996) |
問 6.48 (三角関数の定積分)
自然数
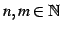 に対して
に対して
となることを示せ(ヒント:積和の公式). ただし,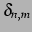 はクロネッカーのデルタ(Kronecker's
delta) である.
はクロネッカーのデルタ(Kronecker's
delta) である.
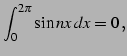 |
(997) | |
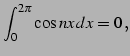 |
(998) | |
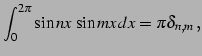 |
(999) | |
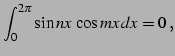 |
(1000) | |
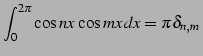 |
(1001) |
となることを示せ(ヒント:積和の公式). ただし,
例 6.50 (双曲線関数を用いた定積分)
定積分
を考える. 積分区間が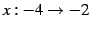 であるから
であるから 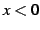 である.
このことに注意して変数変換を
である.
このことに注意して変数変換を
とする.このとき積分区間は
となる.また
であることを用いると
となる.ここで
であることを用いる.このとき
より
となる.また
である.よって
を得る.
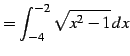 |
(1004) |
を考える. 積分区間が
| (1005) |
とする.このとき積分区間は
| (1006) |
となる.また
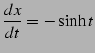 |
(1007) |
であることを用いると
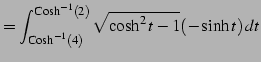 |
(1008) | |
| (積分区間をひっくり返す.
|
(1009) | |
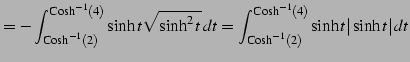 |
(1010) | |
| (
|
(1011) | |
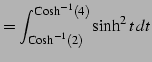 |
(1012) | |
| (
|
(1013) | |
![$\displaystyle = \frac{1}{2} \int^{\mathrm{Cosh}^{-1}(4)}_{\mathrm{Cosh}^{-1}(2)...
... \frac{1}{2}\sinh(2t)-t \right]^{\mathrm{Cosh}^{-1}(4)}_{\mathrm{Cosh}^{-1}(2)}$](img2934.png) |
(1014) | |
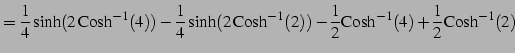 |
(1015) |
となる.ここで
| (1016) |
であることを用いる.このとき
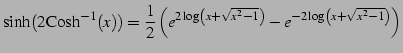 |
(1017) | |
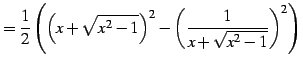 |
(1018) | |
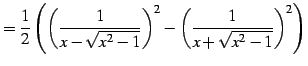 |
(1019) | |
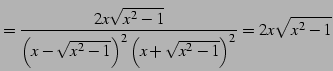 |
(1020) |
より
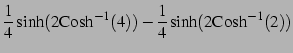 |
 |
(1021) |
| (1022) |
となる.また
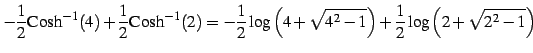 |
(1023) | |
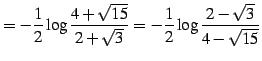 |
(1024) |
である.よって
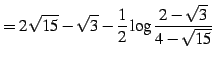 |
(1025) |
を得る.
Next: 14 図形の面積 Up: 6 積分法 Previous: 12 定積分と不定積分 Contents
Kondo Koichi

Created at 2004/08/14
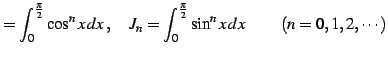
![$\displaystyle I_{n}=J_{n}= \frac{(n-1)!!}{n!!}\varepsilon_{n}\,,\qquad \varepsi...
...($n$: 偶数)} \\ [2ex] \displaystyle{1} & \text{($n$: 奇数)} \end{array} \right.$](img2918.png)