16 回転体の体積

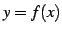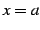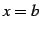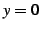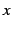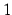定理 6.57 (回転体の体積)   曲線 $y=f(x)$ と直線 $x=a$, $x=b$, $y=0$ とで囲まれてできる図形を $x$ 軸の回りで $1$ 回転してできる立体の体積は

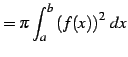$$V = \pi\int_{a}^{b}\left(f(x)\right)^2\,dx$$ (1061)

により求まる．

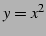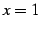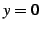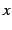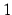例 6.58 (回転体の体積)   $y=x^2$ と $x=1$, $y=0$ とで囲まれてできる領域を $x$ 軸の回りで $1$ 回転してできる立体の体積は

$$V = \pi\int_{0}^{1}\left(x^2\right)^2\,dx= \pi\int_{0}^{1}x^4\,dx= \left[\frac{x^5}{5}\right]_{0}^{1}= \frac{\pi}{5}\,.$$ (1062)

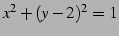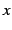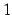問 6.59 (回転体の体積)   $x^2+(y-2)^2=1$ の内部の領域を $x$ 軸の回りで $1$ 回転してできる立体の 体積を求めよ．

Kondo Koichi
Created at 2004/08/14