Next: 25 直線の平面への射影 Up: 1 ベクトルと図形 Previous: 23 点の平面への射影 Contents
24 点と平面との距離
定義 1.111 (点と平面との距離)
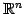 空間内の点
空間内の点 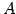 と平面を考える.
点
と平面を考える.
点  と平面上の点
と平面上の点 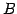 との距離が最小となるとき,
その距離を点と平面との距離という.
との距離が最小となるとき,
その距離を点と平面との距離という.
定理 1.112 (点と平面との距離)
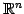 空間内の点
空間内の点 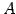 と平面を考える.
点
と平面を考える.
点  と平面上の点
と平面上の点 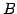 との距離が最小となるのは
直線
との距離が最小となるのは
直線 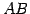 と平面が直交するときである.
と平面が直交するときである.
例 1.113 (点と平面との距離)
点  の平面
の平面
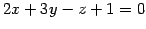 への
射影点は
への
射影点は
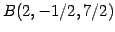 である.
直線
である.
直線 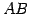 は平面に直交する.
距離
は平面に直交する.
距離
 が点と平面との距離である.
よって距離は
が点と平面との距離である.
よって距離は
である.
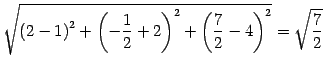 |
(191) |
である.
定理 1.114 (点と平面との距離)
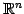 空間内の点
空間内の点
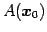 と
平面
と
平面
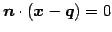 を考える.
点
を考える.
点  と平面との距離は
と平面との距離は
である.
 |
(192) |
である.
問 1.115 (点と平面との距離)
これを示せ.
であるから,
より,
を得る.
(証明)
点
![]() から平面
から平面
![]() への
射影点を
への
射影点を
![]() とする.
距離
とする.
距離
![]() が
点と平面の距離である.
射影点
が
点と平面の距離である.
射影点
![]() は
は
 |
(193) |
であるから,
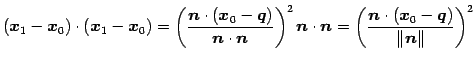 |
(194) |
より,
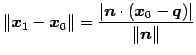 |
(195) |
を得る.
定理 1.116 (
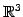 の点と平面との距離)
の点と平面との距離)
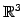 空間内の点
空間内の点
 と
平面
と
平面
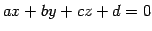 を考える.
点
を考える.
点 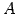 と平面との距離は
と平面との距離は
である.
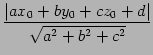 |
(196) |
である.
問 1.117 (
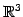 の点と平面との距離)
これを示せ.
の点と平面との距離)
これを示せ.
とおく.
より,
を得る.
(証明)
点
![]() と平面
と平面
![]() とし,
とし,
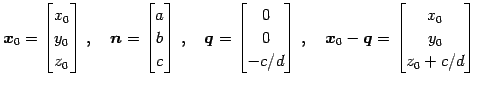 |
(197) |
とおく.
| (198) |
より,
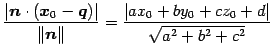 |
(199) |
を得る.
例 1.118 (
 の点と平面との距離)
点
の点と平面との距離)
点  の平面
の平面
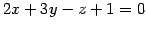 との距離は
との距離は
である.
 |
(200) |
である.
Next: 25 直線の平面への射影 Up: 1 ベクトルと図形 Previous: 23 点の平面への射影 Contents
Kondo Koichi

Created at 2004/11/26