Next: 16 部分空間 Up: 1 ベクトル空間 Previous: 14 1 次結合の記法 Contents
15 1 次独立なベクトルの最大個数
定義 1.64 (ベクトルの 1 次独立な最大個数)
ベクトルの集合 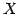 が,
ある
が,
ある 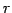 個のベクトルでは 1 次独立となり,
任意の
個のベクトルでは 1 次独立となり,
任意の 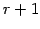 個のベクトルでは 1 次従属となるとき,
個のベクトルでは 1 次従属となるとき,
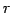 を集合
を集合 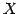 の
1 次独立なベクトルの最大個数という.
の
1 次独立なベクトルの最大個数という.
例 1.65 (ベクトルの 1 次独立な最大個数の具体例)
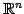 の 1 次独立なベクトルの最大個数は
の 1 次独立なベクトルの最大個数は 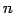 である.
である.
を 1 次独立と仮定する. このとき 1 次関係
を考える. これより
となる. 係数行列の階数は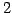 以下であるから
以下であるから
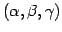 は任意定数を含む解であり,
1 次関係は非自明係数となる.
よって,
は任意定数を含む解であり,
1 次関係は非自明係数となる.
よって,
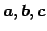 は
1 次従属である.
以上より,
は
1 次従属である.
以上より,
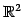 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は 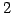 である.
である.
(証明)
![]() のときを考える.
まず明らかに
のときを考える.
まず明らかに
![]() は 1 次独立であるので,
1 次独立なベクトルの最大個数は 2 以上である.
ここで,3 個のベクトル
は 1 次独立であるので,
1 次独立なベクトルの最大個数は 2 以上である.
ここで,3 個のベクトル
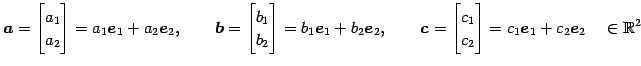 |
を 1 次独立と仮定する. このとき 1 次関係
を考える. これより
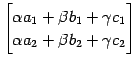 |
||
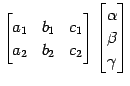 |
となる. 係数行列の階数は
![]() のときも同様に示される.
のときも同様に示される.
定理 1.66 (簡約化行列の 1 次関係)
行列
を簡約化した行列を
とする. このとき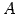 の列ベクトル
の列ベクトル
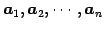 に関する
1 次関係と
に関する
1 次関係と 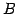 の列ベクトル
の列ベクトル
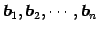 に関する
1 次関係とは等価である.
に関する
1 次関係とは等価である.
と表される. これは
となるので,各列ベクトルは
と表される.また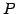 は正則行列であるから,
は正則行列であるから,
とも表される. ここで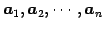 に関する
1 次関係を
に関する
1 次関係を
とする.これより,
を得る. これは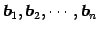 に関する 1 次関係であり,
に関する 1 次関係であり,
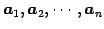 に関する 1 次関係と
等しい.
に関する 1 次関係と
等しい.
を簡約化した行列を
とする. このとき
(証明)
行列 ![]() を簡約化して
を簡約化して ![]() となるとき,
基本変形を表す行列
となるとき,
基本変形を表す行列 ![]() を用いて
を用いて
と表される. これは
となるので,各列ベクトルは
と表される.また
とも表される. ここで
とする.これより,
を得る. これは
例 1.67 (ベクトルの 1 次独立な最大個数の具体例)
ベクトル
の 1 次独立なベクトルの最大個数と そのときベクトルの組の一つを求める. また,その他のベクトルを 1 次独立なベクトルの 1 次結合で表す.
を考える.これは
と表される. 方程式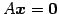 の解を求めることで,
1 次関係の係数
の解を求めることで,
1 次関係の係数 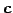 が定まる.
行列
が定まる.
行列 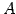 を簡約化すると
を簡約化すると
となる. 方程式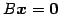 の解もまた
の解もまた 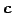 となる.
なすわち,
ベクトル
となる.
なすわち,
ベクトル
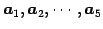 の 1 次関係と
ベクトル
の 1 次関係と
ベクトル
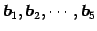 の 1 次関係
の 1 次関係
は同じものである. まず,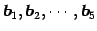 の
1 次独立なベクトルの最大個数を考える.
の
1 次独立なベクトルの最大個数を考える.
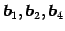 に着目すると,
に着目すると,
であり,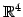 の基本ベクトルである.
明らかにこれらは 1 次独立であるので,
1 次独立なベクトルの最大個数は少なくとも
の基本ベクトルである.
明らかにこれらは 1 次独立であるので,
1 次独立なベクトルの最大個数は少なくとも 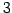 である.
他のベクトル
である.
他のベクトル
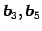 について見ると
について見ると
である.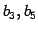 は 1 次従属である.
よってベクトル
は 1 次従属である.
よってベクトル
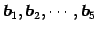 の
1 次独立なベクトルの最大個数は
の
1 次独立なベクトルの最大個数は
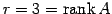 であり,
その 1 次独立なベクトルの組の一つは
であり,
その 1 次独立なベクトルの組の一つは
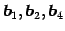 である.
またその他のベクトルは
である.
またその他のベクトルは
と 1 次結合で表される. これらの結果は ベクトル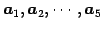 の
1 次関係にも適用される.
1 次独立なベクトルの最大個数は
の
1 次関係にも適用される.
1 次独立なベクトルの最大個数は
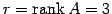 であり,
そのベクトルの組は
であり,
そのベクトルの組は
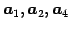 である.
また,その他のベクトルは
である.
また,その他のベクトルは
が成り立つ.
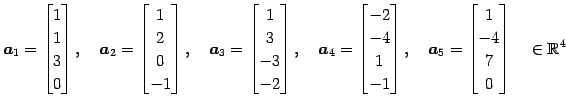 |
の 1 次独立なベクトルの最大個数と そのときベクトルの組の一つを求める. また,その他のベクトルを 1 次独立なベクトルの 1 次結合で表す.
ベクトル
![]() の 1 次関係
の 1 次関係
を考える.これは
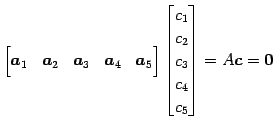 |
と表される. 方程式
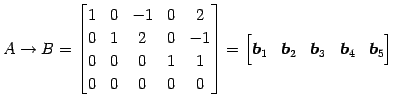 |
となる. 方程式
は同じものである. まず,
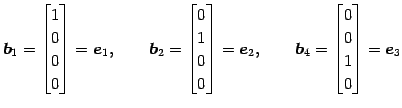 |
であり,
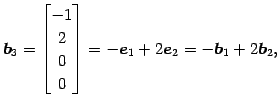 |
||
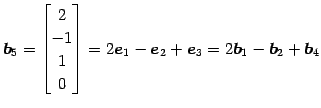 |
である.
と 1 次結合で表される. これらの結果は ベクトル
が成り立つ.
定理 1.68 (行列の列ベクトルと行ベクトルの 1 次独立な最大個数)
定理 1.69 (行列と 1 次独立性)
正方行列
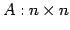 に対して次の関係が成り立つ:
に対して次の関係が成り立つ:
| |
||
| |
||
| |
||
Next: 16 部分空間 Up: 1 ベクトル空間 Previous: 14 1 次結合の記法 Contents
Kondo Koichi

Created at 2004/12/13