Next: 17 ベクトルで張られる空間 Up: 1 ベクトル空間 Previous: 15 1 次独立なベクトルの最大個数 Contents
16 部分空間
定義 1.70 (部分空間)
ベクトル空間 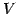 の部分集合
の部分集合 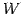 がベクトル空間となるとき,
がベクトル空間となるとき,
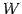 を
を 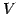 の部分空間(subspace)という.
の部分空間(subspace)という.
定理 1.71 (部分空間)
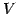 の部分集合
の部分集合 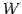 が
が 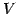 の部分空間となるための
必用十分条件は,
すべての
の部分空間となるための
必用十分条件は,
すべての
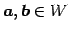 と
と
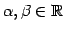 に対して
に対して
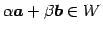 をみたすことである.
をみたすことである.
注意 1.72 (部分空間と零ベクトル)
部分空間 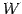 は零ベクトル
は零ベクトル 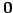 を含む.
なぜなら,
部分空間の必用十分条件で
を含む.
なぜなら,
部分空間の必用十分条件で
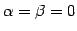 とおくと
とおくと
となるからである.
となるからである.
例 1.73 (部分空間の具体例)
連立方程式
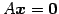 の解の集合
の解の集合
は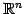 の部分空間である.
一方,
連立方程式
の部分空間である.
一方,
連立方程式
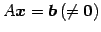 の解の集合
の解の集合
は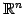 の部分空間ではない.
の部分空間ではない.
は
は
(証明) 解空間の節を参照.
例 1.74 (部分空間ではない具体例)
集合
は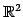 の部分空間ではない.
なぜなら,
の部分空間ではない.
なぜなら,
に対して
となるからである.
は
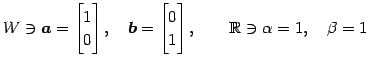 |
に対して
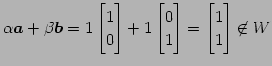 |
となるからである.
例 1.75 (部分空間ではない具体例)
集合
は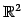 の部分空間ではない.
なぜなら,
の部分空間ではない.
なぜなら,
に対して
となるからである.
は
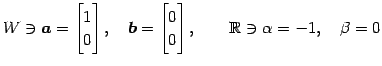 |
に対して
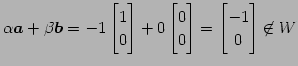 |
となるからである.
Next: 17 ベクトルで張られる空間 Up: 1 ベクトル空間 Previous: 15 1 次独立なベクトルの最大個数 Contents
Kondo Koichi

Created at 2004/12/13