Next: 20 正規直交基底 Up: 1 ベクトル空間 Previous: 18 基底 Contents
19 次元
定理 1.84 (ベクトル空間の基底の個数)
ベクトル空間の基底の個数は取り方に依らず一意に定まる.
その個数は,
ベクトル空間に含まれる 1 次独立なベクトルの最大個数と等しい.
定義 1.85 (次元)
ベクトル空間 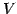 の基底の個数が
の基底の個数が 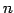 個であるとき,
これをベクトル空間
個であるとき,
これをベクトル空間 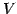 の次元(dimension)と呼び,
の次元(dimension)と呼び,
と表記する.
と表記する.
例 1.86 (ベクトル空間の次元の具体例)
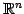 は標準基底
は標準基底
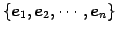 を
用いて
を
用いて
と表されるので,次元は
となる.
と表されるので,次元は
となる.
定理 1.87 (ベクトル空間の次元と階数)
部分空間
の次元は
である.
の次元は
である.
定理 1.88 (部分空間の次元)
ベクトル空間 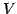 ,
, 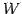 が
が
であるとき,
が成り立つ.
であるとき,
が成り立つ.
例 1.89 (部分空間の次元の具体例)
ベクトル
を用いて生成される部分空間
の次元を求める.
となる.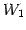 は原点
は原点
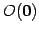 と点
と点
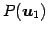 を通る直線である.
を通る直線である.
であるから,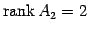 であり,
であり,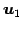 ,
, 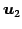 は
1 次独立となる.
よって
は
1 次独立となる.
よって 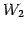 の基底は
の基底は
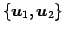 であり,
であり,
を得る.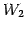 は原点
は原点
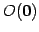 と点
と点
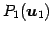 ,
,
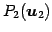 を通る平面である.
を通る平面である.
であるから,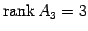 であり,
であり,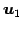 ,
, 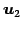 ,
, 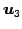 は
1 次独立となる.
よって
は
1 次独立となる.
よって 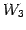 の基底は
の基底は
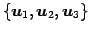 であり,
であり,
を得る.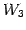 は 3 本の軸がそれぞれ
点
は 3 本の軸がそれぞれ
点
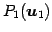 ,
,
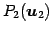 ,
,
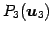 を
通る 3 次元空間である.
を
通る 3 次元空間である.
であるから,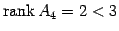 であり,
であり,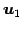 ,
, 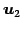 ,
, 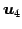 は
1 次従属となる.
最大個数となる 1 次独立なベクトルは
は
1 次従属となる.
最大個数となる 1 次独立なベクトルは
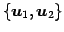 であり,
その他のベクトルは
であり,
その他のベクトルは
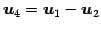 と表される.
よって
と表される.
よって 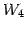 の基底は
の基底は
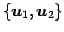 であり,
であり,
となる.以上より
を得る.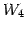 は平面
は平面 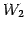 と等しい.
点
と等しい.
点
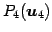 は平面
は平面 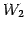 に含まれる点であるためである.
に含まれる点であるためである.
であるから,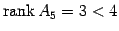 であり,
であり,
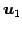 ,
, 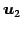 ,
, 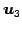 ,
, 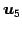 は 1 次従属となる.
最大個数となる 1 次独立なベクトルは
は 1 次従属となる.
最大個数となる 1 次独立なベクトルは
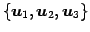 であり,
その他のベクトルは
であり,
その他のベクトルは
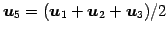 と表される.
よって
と表される.
よって 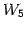 の基底は
の基底は
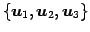 であり,
であり,
となる.以上より
を得る.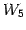 は
は 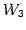 と等しい.
と等しい.
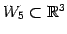 であるから,
であるから,
となることを注意する.
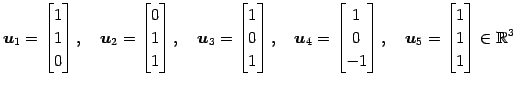 |
を用いて生成される部分空間
の次元を求める.
(1) ![]() の基底は
の基底は
![]() である.よって
である.よって
となる.
(2) ![]() の基底をまず求める.
の基底をまず求める.
![]() ,
, ![]() が 1 次独立であるか調べる.
が 1 次独立であるか調べる.
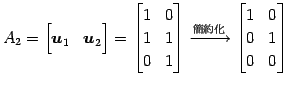 |
であるから,
を得る.
(3) ![]() の基底をまず求める.
の基底をまず求める.
![]() が 1 次独立であるか調べる.
が 1 次独立であるか調べる.
 |
であるから,
を得る.
(4) ![]() の基底をまず求める.
の基底をまず求める.
![]() が 1 次独立であるか調べる.
が 1 次独立であるか調べる.
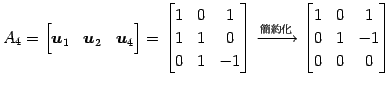 |
であるから,
となる.以上より
を得る.
(5) ![]() の基底をまず求める.
の基底をまず求める.
![]() が 1 次独立であるか調べる.
が 1 次独立であるか調べる.
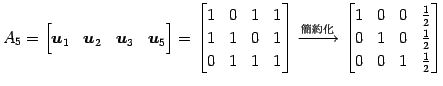 |
であるから,
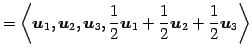 |
||
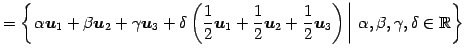 |
||
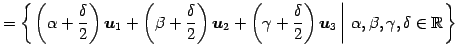 |
||
となる.以上より
を得る.
となることを注意する.
Next: 20 正規直交基底 Up: 1 ベクトル空間 Previous: 18 基底 Contents
Kondo Koichi

Created at 2004/12/13