Next: 17 直線の線形変換 Up: 2 線形写像 Previous: 15 線形写像の像と核 Contents
16 線形写像の階数と退化次数
定義 2.67 (退化次数,階数)
像
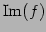 の次元を階数(rank)といい,
の次元を階数(rank)といい,
と定義する. また,核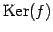 の次元を退化次数(nullity)といい,
の次元を退化次数(nullity)といい,
と定義する.
と定義する. また,核
と定義する.
定理 2.68 (退化次数,階数)
線形写像
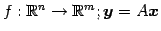 の階数は
の階数は
であり,退化次数は
である.
であり,退化次数は
である.
(証明)
定理 2.69 (退化次数,階数)
線形写像 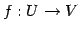 に関して
に関して
が成立する.
が成立する.
(証明)
例 2.70 (線形写像の像と核の具体例)
線形写像
の像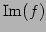 ,核
,核
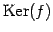 と
それらの次元
と
それらの次元
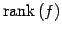 ,
,
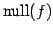 を求める.
を求める.
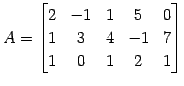 |
の像
Kondo Koichi

Created at 2004/12/13