2.26 関数の極限の確定と不確定
定義 2.80 (無限大)
変数 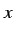 の値が正で限りなく大きくなるとき
の値が正で限りなく大きくなるとき
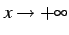 と書く.
変数
と書く.
変数 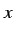 の値が負で限りなく小さくなるとき
の値が負で限りなく小さくなるとき
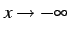 と書く.
また,
変数
と書く.
また,
変数 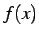 の値が正で限りなく大きくなるとき
の値が正で限りなく大きくなるとき
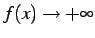 と書く.
変数
と書く.
変数 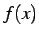 の値が負で限りなく小さくなるとき
の値が負で限りなく小さくなるとき
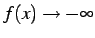 と書く.
と書く.
例 2.81 (無限大の具体例)
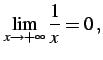 |
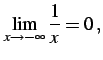 |
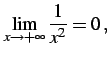 |
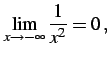 |
(156) | ||||
| (157) | ||||||||
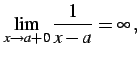 |
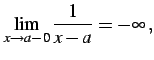 |
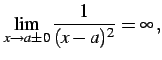 |
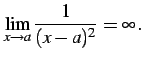 |
(158) |
注意 2.82 (確定,不確定)
極限
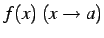 を特徴づける性質として,
収束,発散以外にも次の条件を考える:
を特徴づける性質として,
収束,発散以外にも次の条件を考える:
| 収束 | 有限確定 | 確定 |
(例)
|
| 発散 | 無限確定 | 確定 |
(例)
|
| 発散 | 無限不確定 | 不確定 |
(例)
|
| 発散 | 有限不確定 | 不確定 |
(例)
|
注意 2.83 (不定形)
極限操作をし不定形
と呼ばれる形になるときは注意が必要である. このままではまだ有限確定とも無限確定とも分からない. もしこの形のになるときは式変形をした後に極限操作を行う. 極限が有限確定または無限確定
するように計算方法を工夫する.
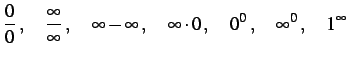 |
(159) |
と呼ばれる形になるときは注意が必要である. このままではまだ有限確定とも無限確定とも分からない. もしこの形のになるときは式変形をした後に極限操作を行う. 極限が有限確定または無限確定
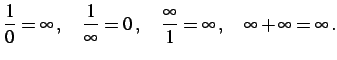 |
(160) |
するように計算方法を工夫する.
例 2.84 (関数の極限の計算例)
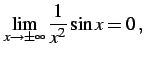 |
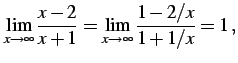 |
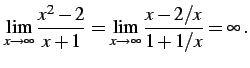 |
(161) |
Kondo Koichi

平成17年8月31日