2.17 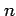 変数関数と 1 変数関数の合成関数の微分
変数関数と 1 変数関数の合成関数の微分
定理 2.72 (多変数関数の合成関数の微分)
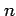 変数関数
変数関数
 と
1 変数関数
と
1 変数関数
の合成関数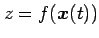 の微分は
の微分は
で与えられる.代入も含めて書くと
となる. また,ベクトル表記では
と表される. ここで
とおいた.
の合成関数
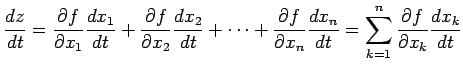 |
で与えられる.代入も含めて書くと
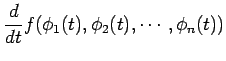 |
||
となる. また,ベクトル表記では
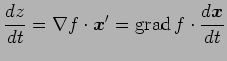 |
と表される. ここで
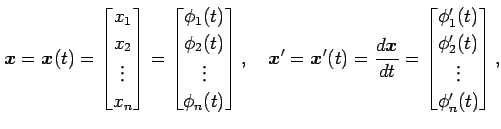 |
||
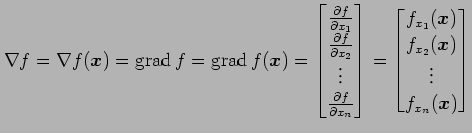 |
とおいた.
注意 2.73 (多変数関数の合成関数の微分)
曲面
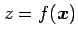 の点
の点 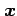 における
法線ベクトルは
における
法線ベクトルは
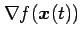 である(接平面の節を参照).
である(接平面の節を参照).
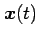 の軌跡は
の軌跡は
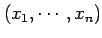 空間内の曲線である.
この曲線の接ベクトルは
空間内の曲線である.
この曲線の接ベクトルは
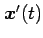 である.
である.
Kondo Koichi

平成18年1月18日