1.2
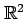 の直線
の直線
注意 1.5 (直線の方程式)
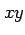 平面内の直線の方程式は
平面内の直線の方程式は
と表される.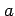 は傾きを表し,
は傾きを表し,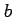 は
は 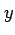 切片である.
また,式変形して
切片である.
また,式変形して
と表すと,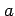 は
は 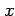 切片であり,
切片であり,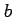 は
は 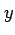 切片を表す.
式変形すると様々な意味をもつ.
通常,直線の方程式の標準形は,
非同次 1 次方程式
切片を表す.
式変形すると様々な意味をもつ.
通常,直線の方程式の標準形は,
非同次 1 次方程式
の形で表す.
と表される.
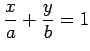 |
と表すと,
の形で表す.
注意 1.6 (直線の方程式と方向ベクトル)
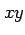 平面内の直線を
平面内の直線を
と表す.このとき, パラメータ を用いてベクトルで表記すると
を用いてベクトルで表記すると
とパラメータ表示される.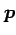 は直線の向きを表し,
方向ベクトル(direction vector)という.
は直線の向きを表し,
方向ベクトル(direction vector)という.
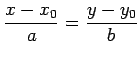 |
と表す.このとき, パラメータ
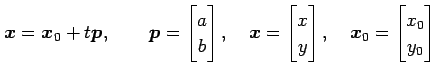 |
とパラメータ表示される.
注意 1.7 (直線の方程式と法線ベクトル)
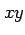 平面内の直線を
平面内の直線を
と表す.このとき,ベクトルで表記すると
と表される.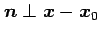 であり,
であり,
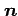 は直線に直交するベクトルである.
は直線に直交するベクトルである.
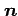 を法線ベクトル(normal vector)という.
を法線ベクトル(normal vector)という.
と表す.このとき,ベクトルで表記すると
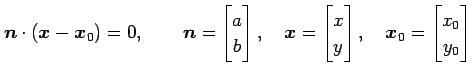 |
と表される.
例 1.8 (直線)
2 点 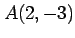 ,
, 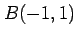 を通る直線を考える.
この直線の方向ベクトルは
を通る直線を考える.
この直線の方向ベクトルは
である.直線の方程式のパラメータ表示は
である.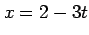 ,
, 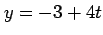 で
で  を消去すると
を消去すると
となる.式変形して
とする. この式より,この直線は法線ベクトルが
で点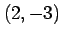 を通る直線である.
さらに式変形して一般形で表すと
を通る直線である.
さらに式変形して一般形で表すと
である. また,式変形して
とする. 直線の傾きは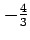 であり,
であり,
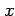 切片は
切片は
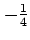 で
で
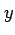 切片は
切片は
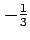 である.
である.
である.式変形すれば
と書ける. 法線は傾きが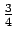 で,
で,
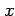 切片が
切片が 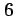 で,
で,
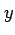 切片が
切片が
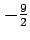 で,
法線ベクトルが
で,
法線ベクトルが
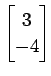 である.
である.
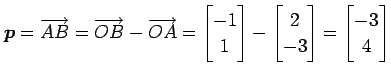 |
である.直線の方程式のパラメータ表示は
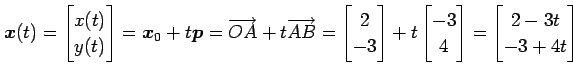 |
である.
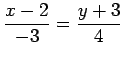 |
となる.式変形して
とする. この式より,この直線は法線ベクトルが
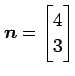 |
で点
である. また,式変形して
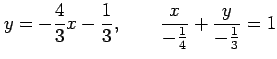 |
とする. 直線の傾きは
次にこの直線と直交し点 ![]() を通る直線を考える.
法線ベクトル
を通る直線を考える.
法線ベクトル ![]() が方向ベクトルとるので,
法線の方程式は
が方向ベクトルとるので,
法線の方程式は
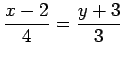 |
である.式変形すれば
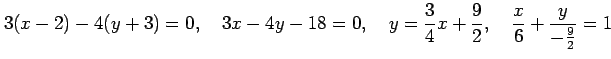 |
と書ける. 法線は傾きが
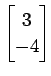 である.
である.
Kondo Koichi

平成18年1月18日