3.14 有向曲線
定義 3.64 (有向曲線)
向き付きの曲線
を有向曲線(oriented curve)という.
を有向曲線(oriented curve)という.
注意 3.65 (有向曲線)
始点と終点が同じであり,有向曲線が一周してもよい.
 |
 |
| (a) 有向曲線 | (b) 始点と終点が同じ有向曲線 |
例 3.66 (有向曲線)
始点 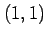 から終点
から終点 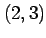 まで
直線的に進む有向曲線は,
まで
直線的に進む有向曲線は,
と書ける.
と書ける.
例 3.67 (有向曲線)
単位円上を始点を 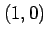 で反時計回りに一周するとき,
で反時計回りに一周するとき,
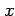 ,
, 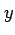 をパラメータ表示すると
をパラメータ表示すると
となる. この有向曲線は
と書ける. 時計回りに一周するときは, 有向曲線は
と書ける.
となる. この有向曲線は
と書ける. 時計回りに一周するときは, 有向曲線は
と書ける.
定義 3.68 (有向曲線)
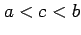 において,
において,
であるとき,
と表記する.
であるとき,
と表記する.

定義 3.69 (有向曲線)
有向曲線
に対して,
と表記する.
に対して,
と表記する.

Kondo Koichi

平成18年1月18日