1.10 ノルム
定義 1.53 (ノルム)
ベクトル
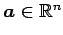 に対して,
に対して,
をベクトル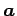 のノルム(norm)または
長さ(length)という.
また,
ベクトル
のノルム(norm)または
長さ(length)という.
また,
ベクトル
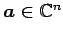 に対しては
に対しては
と定義する.
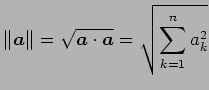 |
(72) |
をベクトル
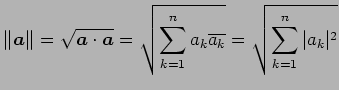 |
(73) |
と定義する.
例 1.54 (ノルムの具体例)
ベクトル
のノルムはそれぞれ
である.
 |
(74) |
のノルムはそれぞれ
| (75) | ||
| (76) |
である.
例 1.55 (ノルムの具体例)
ベクトル
のノルムはそれぞれ
である.
 |
(77) |
のノルムはそれぞれ
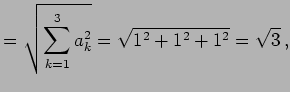 |
(78) | |
 |
(79) |
である.
例 1.56 (ノルムの具体例)
ベクトル
のノルムはそれぞれ
である.
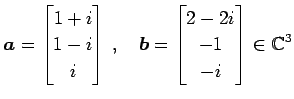 |
(80) |
のノルムはそれぞれ
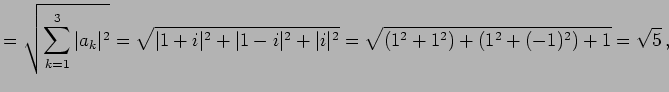 |
(81) | |
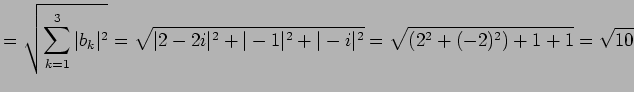 |
(82) |
である.
定理 1.57 (ノルムの性質)
シュバルツの不等式(Schwartz' inequality):
三角不等式(triangle inequality???):
| (83) |
三角不等式(triangle inequality???):
| (84) |
Kondo Koichi

平成17年9月15日