5.15 2 次正方行列の対角化
例 5.42 (対角化の具体例)
行列
を対角化する.
となるので,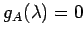 より
より
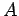 の固有値は
の固有値は
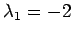 ,
,
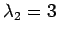 である.
である.
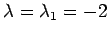 のとき
のとき
より,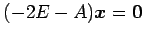 を解いて
固有ベクトルは
を解いて
固有ベクトルは
である.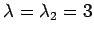 のとき
のとき
より,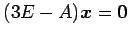 を解いて
固有ベクトルは
を解いて
固有ベクトルは
である.
とおく.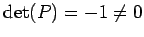 であるから,
であるから,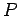 は正則である.
よって,
は正則である.
よって, 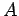 は
は
と対角化される.
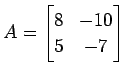 |
を対角化する.
まず,行列 ![]() の固有多項式は
の固有多項式は
 |
となるので,
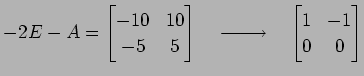 |
より,
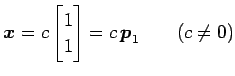 |
である.
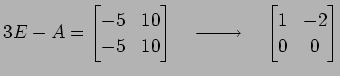 |
より,
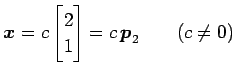 |
である.
行列 ![]() を対角化する.
を対角化する.
![]() の固有ベクトルのひとつとして
の固有ベクトルのひとつとして ![]() を選び,
を選び,
![]() の固有ベクトルのひとつとして
の固有ベクトルのひとつとして ![]() を選ぶ.
このとき
を選ぶ.
このとき
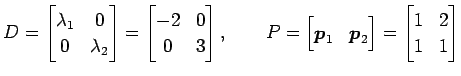 |
とおく.
| (1) |
と対角化される.
問 5.43 (対角化の確認)
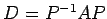 が成立することを
数値を代入して確認せよ.
が成立することを
数値を代入して確認せよ.
注意 5.44 (対角化と固有空間)
線形変換
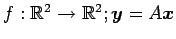 の固有空間は
の固有空間は
である.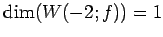 ,
,
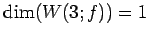 ,
,
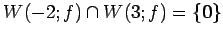 となるので,
となるので,
が成り立つ.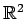 は固有空間に直和分解される.
は固有空間に直和分解される.
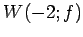 の基底は
の基底は
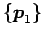 ,
,
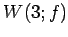 の基底は
の基底は
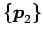 ,
,
 の基底は
の基底は
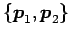 となる.
となる.
である.
が成り立つ.
問 5.45 (固有空間)
固有空間 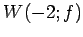 は原点を通り方向ベクトル
は原点を通り方向ベクトル
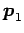 の直線であり,
の直線であり,
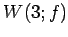 は原点を通り方向ベクトル
は原点を通り方向ベクトル
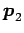 の直線である.
二つの直線のなす角度を求めよ.
の直線である.
二つの直線のなす角度を求めよ.
Kondo Koichi

平成18年1月17日