3.9 演習問題 〜 部分空間
問 3.39 (部分空間)
ベクトル空間
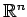 において,
部分集合
において,
部分集合 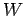 は部分空間であるか述べよ.
は部分空間であるか述べよ.
(1)
![]() (2)
(2)
![]() (ただし,
(ただし,
![]() )
)
(3)
![]() (4)
(4)
![]()
(5)
![]() (
(
![]() はあるベクトル)
はあるベクトル)
(6)
![]()
問 3.40 (部分空間)
ベクトル空間
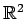 において,
部分集合
において,
部分集合 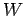 は部分空間であるか述べよ.
は部分空間であるか述べよ.
(1)
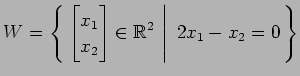 (2)
(2)
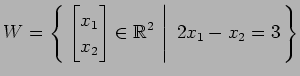
(3)
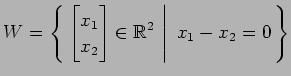 (4)
(4)
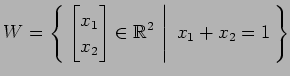
(5)
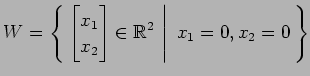 (6)
(6)
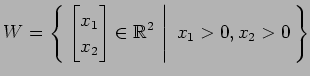
(7)
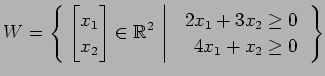 (8)
(8)
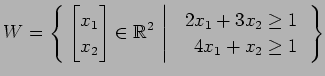
(9)
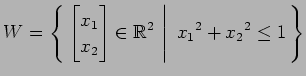 (10)
(10)
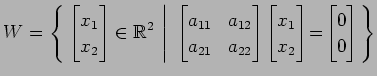
(11)
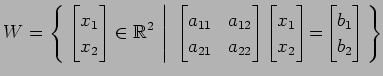
問 3.41 (部分空間)
ベクトル空間
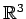 において,
部分集合
において,
部分集合 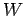 は部分空間であるか述べよ.
は部分空間であるか述べよ.
(1)
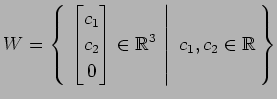 (2)
(2)
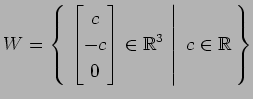
(3)
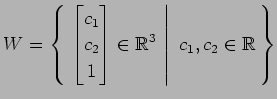 (4)
(4)
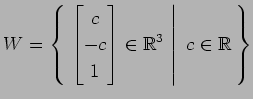
(5)
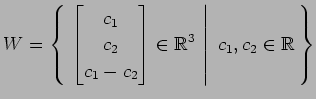 (6)
(6)
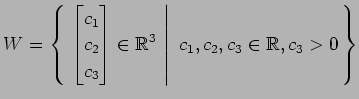 (7)
(7)
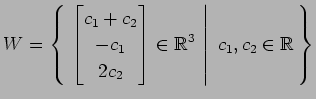 (8)
(8)
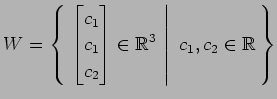
(9)
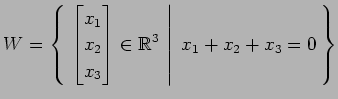 (10)
(10)
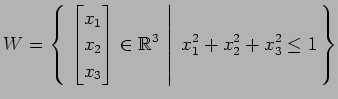
(11)
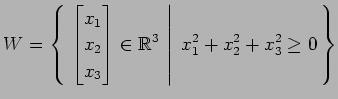 (12)
(12)
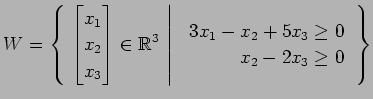 (13)
(13)
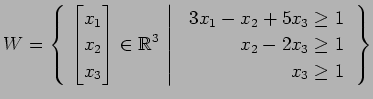
(14)
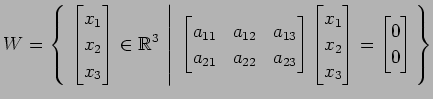
(15)
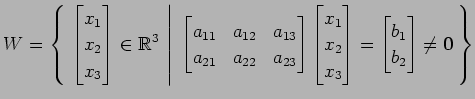
(16)
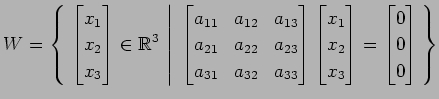
(17)
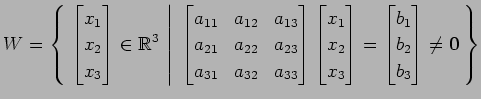
問 3.42 (部分空間)
ベクトル空間
![$ \mathbb{R}[x]_3$](img554.png) において,
部分集合
において,
部分集合 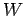 は部分空間であるか述べよ.
は部分空間であるか述べよ.
(1)
![]() (2)
(2)
![]()
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]()
(9)
![]() (10)
(10)
![]()
(11)
![]() (12)
(12)
![]()
(13)
![]()
(14)
![]()
(15)
![]()
(16)
![]()
(17)
![]()
(18)
![]()
Kondo Koichi

平成18年1月17日