3.16 演習問題 〜 1 次独立
問 3.71 (1 次独立)
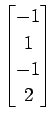
次のベクトルの組が 1 次独立であるか 1 次従属であるか述べよ.
(1)
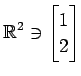 (2)
(2)
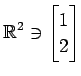 ,
,
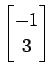 (3)
(3)
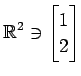 ,
,
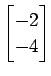 (4)
(4)
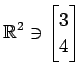 ,
,
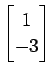
(5)
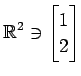 ,
,
![]() ,
,
![]() (6)
(6)
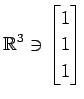 ,
,
![]() ,
,
![]() (7)
(7)
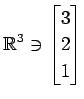 ,
,
![]() ,
,
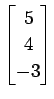
(8)
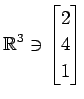 ,
,
![]() ,
,
![]() ,
,
![]() (9)
(9)
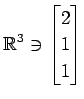 ,
,
![]() ,
,
![]() (10)
(10)
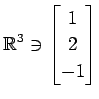 ,
,
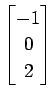
(11)
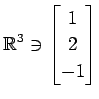 ,
,
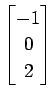 ,
,
 (12)
(12)
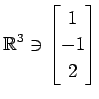 (13)
(13)
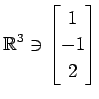 ,
,
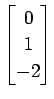
(14)
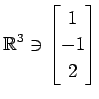 ,
,
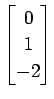 ,
,
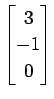 (15)
(15)
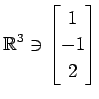 ,
,
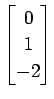 ,
,
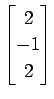
(16)
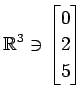 ,
,
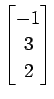 ,
,
![]() ,
,
![]() (17)
(17)
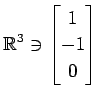 ,
,
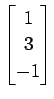 ,
,
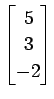
(18)
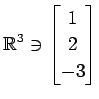 ,
,
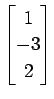 ,
,
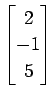 (19)
(19)
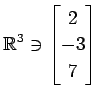 ,
,
![]() ,
,
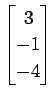
(20)
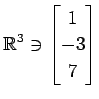 ,
,
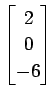 ,
,
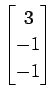 ,
,
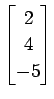 (21)
(21)
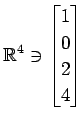 ,
,
![]() ,
,
![]() ,
,
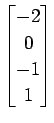
(22)
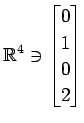 ,
,
![]() (23)
(23)
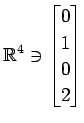 ,
,
![]() ,
,
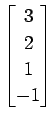 ,
,
 (24)
(24)
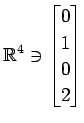 ,
,
![]() ,
,
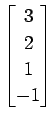 ,
,
 (25)
(25)
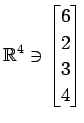 ,
,
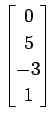 ,
,
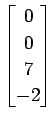
(26)
![]()
問 3.72 (1 次結合)
ベクトルを
とおく.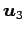 を
を 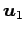 ,
, 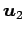 の1 次結合で表せ.
また,
の1 次結合で表せ.
また,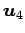 か
か 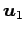 ,
, 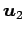 の
1 次結合で表されるための
の
1 次結合で表されるための 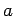 の値を定めよ.
の値を定めよ.
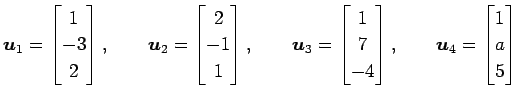 |
とおく.
問 3.73 (1 次独立)
ベクトル
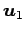 ,
,
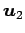 ,
, 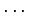 ,
,
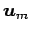 が 1 次独立のとき,
が 1 次独立のとき,
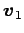 ,
,
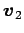 ,
, 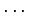 ,
,
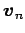 は 1 次独立であるか 1 次従属であるか述べよ.
は 1 次独立であるか 1 次従属であるか述べよ.
(1)
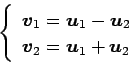 (2)
(2)
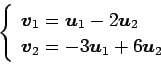 (3)
(3)
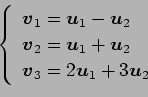
(4)
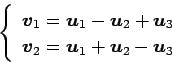 (5)
(5)
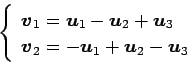 (6)
(6)
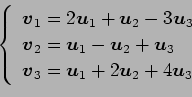
(7)
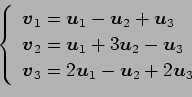 (8)
(8)
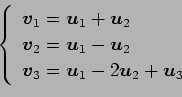 (9)
(9)
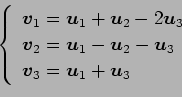 (10)
(10)
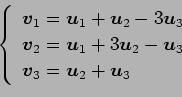 (11)
(11)
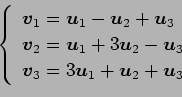 (12)
(12)
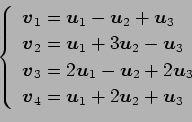 (13)
(13)
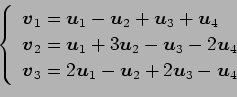 (14)
(14)
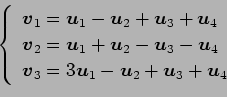
(15)
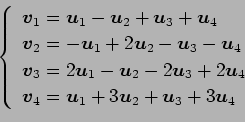 (16)
(16)
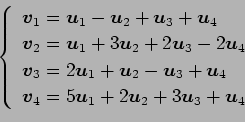
(17)
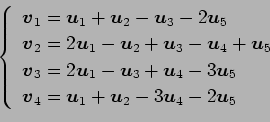 (18)
(18)
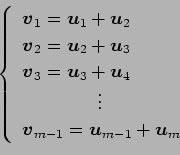 (19)
(19)
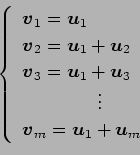
Kondo Koichi

平成18年1月17日