3.31 演習問題 〜 次元
問 3.117 (ベクトルで生成される空間)
次のベクトルで生成される集合が表す図形は何か述べよ.
(1)
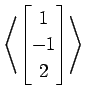 (2)
(2)
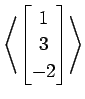 (3)
(3)
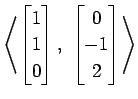 (4)
(4)
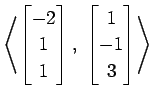
問 3.118 (基底)
次のベクトルの組は基底となるか述べよ.
(1)
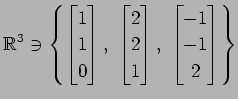 (2)
(2)
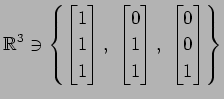
(3)
![]() (4)
(4)
![]()
問 3.119 (基底)
次のベクトルの組が基底となるよう 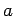 ,
, 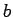 ,
, 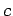 を定めよ.
を定めよ.
(1)
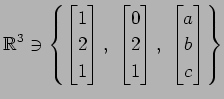 (2)
(2)
![]()
問 3.120 (基底)
ベクトル空間 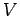 において基底のひとつを
において基底のひとつを
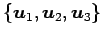 とする.
次のベクトルの組
とする.
次のベクトルの組
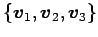 は
は
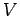 の基底となるか述べよ.
の基底となるか述べよ.
(1)
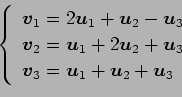 (2)
(2)
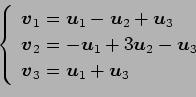
問 3.121 (次元)
次のベクトル空間の次元と基底の組をひとつ求めよ.
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]()
(9)
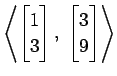 (10)
(10)
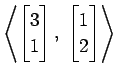 (11)
(11)
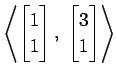 (12)
(12)
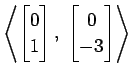
(13)
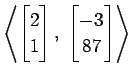 (14)
(14)
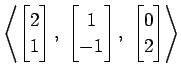 (15)
(15)
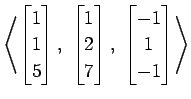
(16)
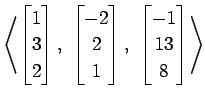 (17)
(17)
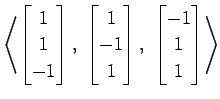 (18)
(18)
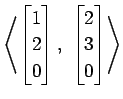
(19)
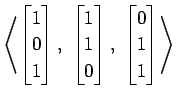 (20)
(20)
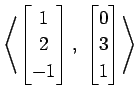 (21)
(21)
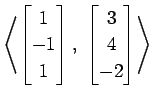
(22)
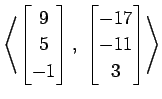 (23)
(23)
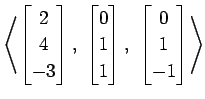 (24)
(24)
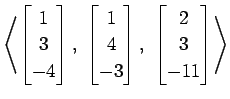
(25)
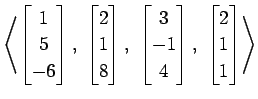 (26)
(26)
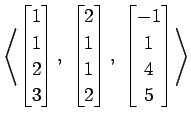
(27)
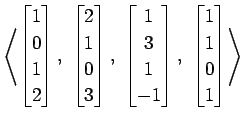 (28)
(28)
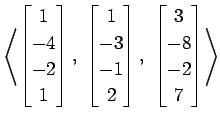
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]()
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]()
(42)
![]() (43)
(43)
![]()
ただし
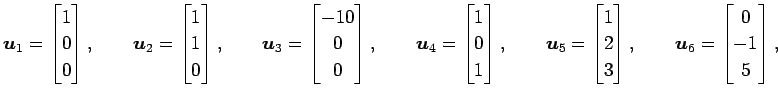 |
||
Kondo Koichi

平成18年1月17日