3.38 正規直交基底
定義 3.147 (正規直交基底)
内積空間の基底
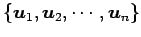 に
対して次の名称を定義する:
に
対して次の名称を定義する:
- 正規基底(normal basis):
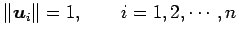
- 直交基底(orthogonal basis):
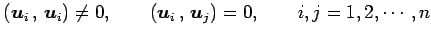
- 正規直交基底(orthonormal basis):
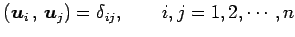
例 3.148 (基本ベクトルの正規直交性)
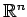 の
標準基底
の
標準基底
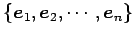 は
正規直交基底である.
は
正規直交基底である.
(証明)
例 3.149 (正規直交基底の具体例)
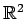 の基底
の基底
は
をみたすので正規直交基底である.
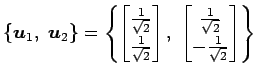 |
は
をみたすので正規直交基底である.
例 3.150 (正規直交基底の具体例)
 の基底
の基底
は
をみたすので正規直交基底である.
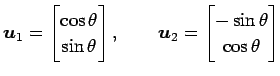 |
は
をみたすので正規直交基底である.
問 3.151 (正規直交基底)
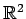 の正規直交基底はすべて
の正規直交基底はすべて
の形で表される.
 |
の形で表される.
Kondo Koichi

平成18年1月17日