3.37 演習問題 〜 座標
問 3.143 (座標)
基底  における
ベクトル
における
ベクトル 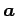 の座標を求めよ.
の座標を求めよ.
(1)
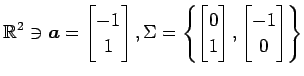 (2)
(2)
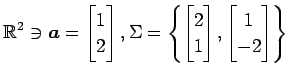
(3)
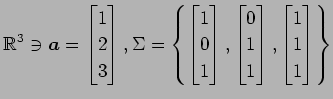 (4)
(4)
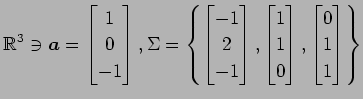
問 3.144 (基底の変換行列)
基底 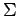 から基底
から基底 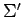 への
基底の変換行列を求めよ.
への
基底の変換行列を求めよ.
(1)
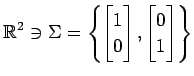 ,
,
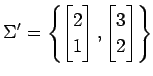 (2)
(2)
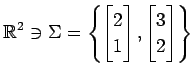 ,
,
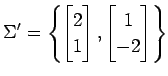
(3)
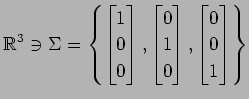 ,
,
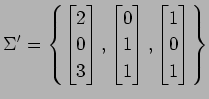
(4)
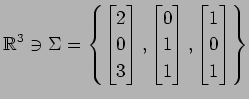 ,
,
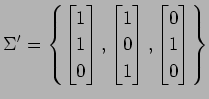
(5)
![]() ,
,
![]()
(6)
![]() ,
,
![]()
問 3.145 (座標変換)
次の座標で与えられるベクトルを求めよ.
また,このベクトルの基底 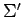 に関する座標を求めよ.
ただし,基底
に関する座標を求めよ.
ただし,基底 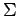 ,
, 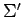 は前問の基底を用いる.
は前問の基底を用いる.
(1)-(2)
![]() (3)-(4)
(3)-(4)
![]() (5)-(6)
(5)-(6)
![]()
問 3.146 (座標変換)
前問の基底 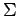 ,
, 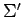 における
座標をそれぞれ
における
座標をそれぞれ
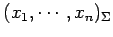 ,
,
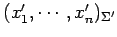 とする.
座標
とする.
座標
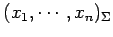 における
直線または平面が次のように与えられるとき,
これらを座標
における
直線または平面が次のように与えられるとき,
これらを座標
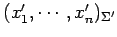 で表せ.
で表せ.
(1)-(2)
![]() (3)-(4)
(3)-(4)
![]()
Kondo Koichi

平成18年1月17日