3.48 演習問題 〜 ベクトル空間の和,直交補空間
問 3.192 (ベクトル空間の和)
次の
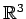 の部分空間
の部分空間 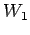 ,
, 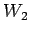 に対して
に対して
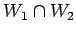 と
と 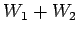 を求めよ.
を求めよ.
(1)
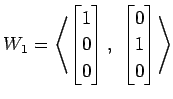 ,
,
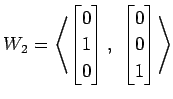 (2)
(2)
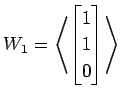 ,
,
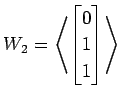
問 3.193 (ベクトル空間の和)
次の部分空間 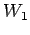 ,
, 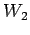 ,
, 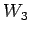 の
和空間
の
和空間
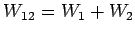 ,
,
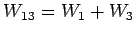 ,
,
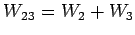 ,
,
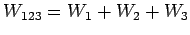 の基底と次元を求めよ.
の基底と次元を求めよ.
 |
問 3.194 (ベクトル空間の和)
次の
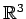 の部分空間
の部分空間 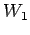 ,
, 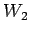 に対して
に対して
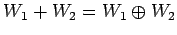 が成り立つか否か示せ.
が成り立つか否か示せ.
(1)
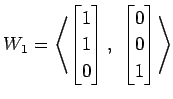 ,
,
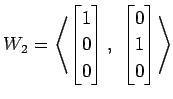 (2)
(2)
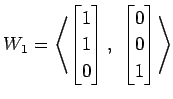 ,
,
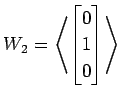
(3)
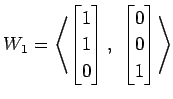 ,
,
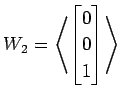 (4)
(4)
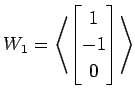 ,
,
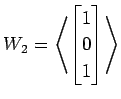
(5)
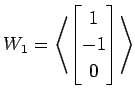 ,
,
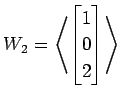
問 3.195 (直交補空間)
次のベクトル空間 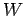 の直交補空間
の直交補空間 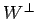 を求めよ.
を求めよ.
(1)
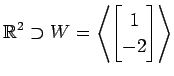 (2)
(2)
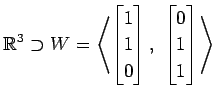 (3)
(3)
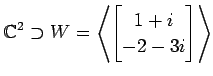 (4)
(4)
![]() (5)
(5)
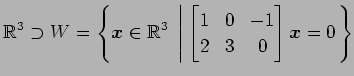
問 3.196 (直交補空間と直和分解)
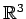 を
を 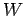 とその直交補空間
とその直交補空間 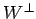 とに直和分解せよ.
とに直和分解せよ.
(1)
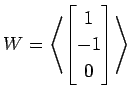 (2)
(2)
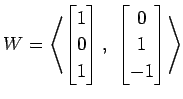 (3)
(3)
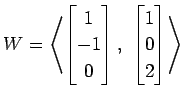
Kondo Koichi

平成18年1月17日