6.13 定積分と不定積分
定理 6.65 (定積分と不定積分の関係)
に対して
が成り立つ.
が成り立つので,
を得る.
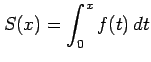 |
に対して
 |
が成り立つ.
(証明)
 |
が成り立つので,
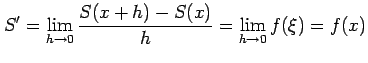 |
を得る.
注意 6.66 (定積分と不定積分の関係)
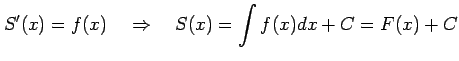 |
定理 6.67 (定積分と不定積分の関係)
関数  の不定積分から得られる原始関数の一つを
の不定積分から得られる原始関数の一つを
とする.このとき の
の  から
から  までの定積分は
までの定積分は
と表される.
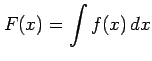 |
とする.このとき
![$\displaystyle \int_{a}^{b}f(x)dx=F(b)-F(a)= \Big[F(x)\Big]_{a}^{b}=F(x)\Big\vert _{x=a}^{x=b}$](img2628.png) |
と表される.
(証明)
 |
例 6.68 (定積分の計算例)
これは長方形の面積を表す.
![$\displaystyle \int_{a}^{b}\alpha\,dx= \alpha\int_{a}^{b}\,dx= \alpha\Big[x\Big]_{a}^{b}= \alpha(b-a)\,.$](img2630.png) |
これは長方形の面積を表す.
例 6.69 (定積分の計算例)
これは台形の面積を表す.
![$\displaystyle \int_{a}^{b}x\,dx= \left[\frac{x^2}{2}\right]_{a}^{b}= \frac{b^2}{2}-\frac{a^2}{2}= \frac{1}{2}(b^2-a^2)= \frac{1}{2}(b-a)(b+a)\,.$](img2631.png) |
これは台形の面積を表す.
例 6.70 (定積分の計算例)
![$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos x\,dx= \Big[\sin x\Big]_{0}^{\frac{\pi}{2}}= \sin\frac{\pi}{2}-\sin 0= 1-0=1\,.$](img2632.png) |
例 6.71 (定積分の計算例)
 |
![$\displaystyle = \Big[\mathrm{Tan}^{-1} x\Big]_{0}^{1}= \mathrm{Tan}^{-1}(1)-\mathrm{Tan}^{-1}(0)= \frac{\pi}{4}-0=\frac{\pi}{4}\,.$](img2634.png) |
例 6.72 (定積分の計算例)
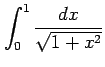 |
Kondo Koichi

平成19年1月23日