4.20 いろいろな行列式
定理 4.108 (ファンデアモントの行列式)
行列式
をファンデアモントの行列式という. は
は
と与えられる.
 |
(821) |
をファンデアモントの行列式という.
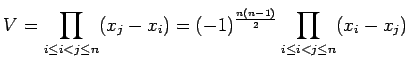 |
(822) |
と与えられる.
問 4.109 (ファンデアモントの行列式)
これを示せ.
とおく. 第 行に
行に 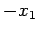 をかけて第
をかけて第  行に加える.
第
行に加える.
第  行に
行に 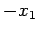 をかけて第
をかけて第  行に加える.
第
行に加える.
第 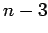 行に
行に 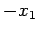 をかけて第
をかけて第  行に加える.
同様に繰り返して,
第
行に加える.
同様に繰り返して,
第 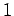 行に
行に 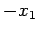 をかけて第
をかけて第  行に加える.
すると
行に加える.
すると
を得る. 第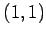 成分で展開すると
成分で展開すると
となる. 第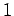 列は
列は
 を共通因子としてもつ.
第
を共通因子としてもつ.
第  列は
列は
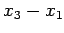 を共通因子としてもつ.
同様にして
第
を共通因子としてもつ.
同様にして
第 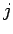 列
列
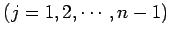 は
は
 を共通因子としてもつ.
共通因子を行列式の外にくくり出すと
を共通因子としてもつ.
共通因子を行列式の外にくくり出すと
である. このとき
が成り立つ. 行列式のサイズがひとつ小さくなった. これを繰り返すと
を得る.
(証明)
行列式を
 |
(823) |
とおく. 第
 |
(824) |
を得る. 第
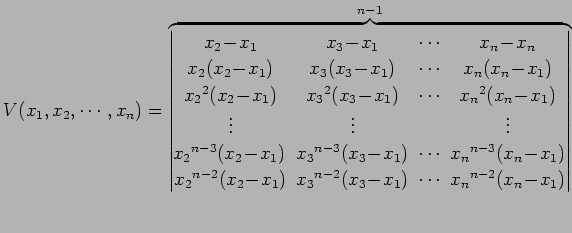 |
(825) |
となる. 第
 |
(826) |
である. このとき
 |
(827) |
が成り立つ. 行列式のサイズがひとつ小さくなった. これを繰り返すと
| (828) | ||
 |
(829) | |
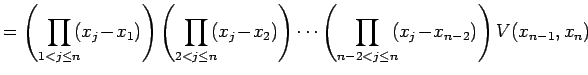 |
(830) | |
 |
(831) | |
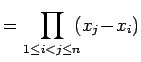 |
(832) |
を得る.
例 4.110 (ファンデアモントの具体例)
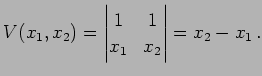 |
(833) | |
 |
(834) | |
 |
(835) | |
| (836) |
定義 4.111 (コンパニオン行列式)
行列式
をコンパニオン行列式(companion determinant)という.
 |
(837) |
をコンパニオン行列式(companion determinant)という.
定理 4.112
コンパニオン行列式は
が成り立つ.
とおく.第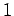 行目を余因子展開すると
行目を余因子展開すると
となる. 前の項の行列式は上三角行列なので対角線分の積で表される. 後の項の行列式はサイズと係数が異なるコンパニオン行列式となる. よって
と表される. これを繰り返すと
を得る.
| (838) |
が成り立つ.
(証明)
行列式を
 |
(839) |
とおく.第
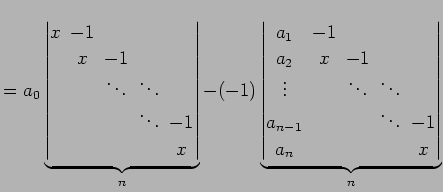 |
(840) |
となる. 前の項の行列式は上三角行列なので対角線分の積で表される. 後の項の行列式はサイズと係数が異なるコンパニオン行列式となる. よって
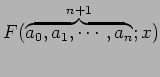 |
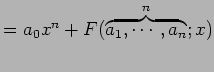 |
(841) |
と表される. これを繰り返すと
 |
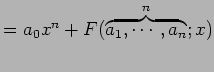 |
(842) |
 |
(843) | |
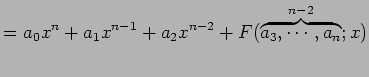 |
(844) | |
 |
(845) | |
| (846) |
を得る.
例 4.113 (コンパニオン行列式の具体例)
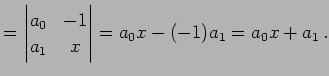 |
(847) | |
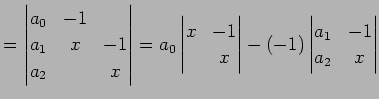 |
(848) | |
| (849) | ||
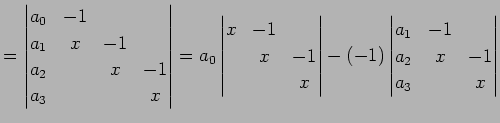 |
(850) | |
| (851) |
問 4.114 (行列式の計算)
となることを示せ.
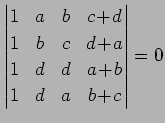 |
(852) |
となることを示せ.
(証明)
 |
(853) |
Kondo Koichi
 KONDO Koichi
KONDO Koichi
平成19年1月25日