1.39 演習問題 〜 平面
問 1.178 (平面)
次の
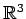 の平面の法線ベクトルと
の平面の法線ベクトルと 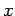 軸,
軸, 軸,
軸, 軸との交点を求めよ.
軸との交点を求めよ.
(1) (2)
(2)  (3)
(3)  (4)
(4) 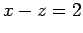
(5) (6)
(6)  (7)
(7) 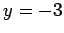 (8)
(8) 
(1)
(5)
問 1.179 (平面)
次の
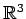 の 3 点を通る平面の方程式を求めよ.
の 3 点を通る平面の方程式を求めよ.
(1) 点 ,
,  ,
,  (2) 点
(2) 点  ,
, 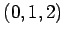 ,
, 
(3) 点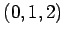 ,
, 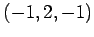 ,
,  (4) 点
(4) 点  ,
, 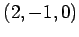 ,
, 
(5) 点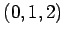 ,
,  ,
, 
(1) 点
(3) 点
(5) 点
問 1.180 (直線と平面の交点)
次の
 の直線と平面の交点を求めよ.
の直線と平面の交点を求めよ.
(1) ,
,

(2)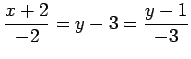 ,
,
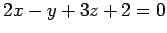
(1)
 ,
,
(2)
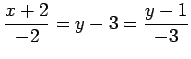 ,
,
問 1.181 (直線と平面の交点)
平面  は平面
は平面  と平行で点
と平行で点 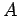 を通るとする.
平面
を通るとする.
平面  の方程式を求めよ.
また,平面
の方程式を求めよ.
また,平面  と直線
と直線 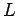 との交点を求めよ.
との交点を求めよ.
(1) :
:
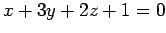 ,
,
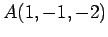 ,
, 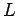 :
:

(2) :
:
 ,
,  ,
, 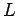 :
:

(1)

(2)

問 1.182 (点の平面への正射影)
次の
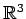 の点から平面への正射影を求めよ.
の点から平面への正射影を求めよ.
(1) ,
,  (2)
(2)
 ,
,

(1)
問 1.183 (点と平面の距離)
次の
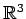 の点と平面の距離を求めよ.
の点と平面の距離を求めよ.
(1)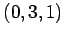 ,
,
 (2)
(2)
 ,
, 
(1)
問 1.184 (平面の交線)
次の
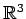 の平面の交線の方向ベクトルを求めよ.
の平面の交線の方向ベクトルを求めよ.
(1) ,
, 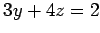 (2)
(2)  ,
, 
(3) ,
,
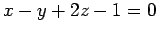 (4)
(4)
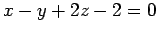 ,
,
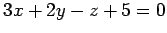
(1)
(3)
問 1.185 (平面と直線)
次の
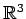 の平面と直交し点
の平面と直交し点 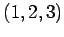 を通る直線の方程式を求めよ.
また,その交点を求めよ.
を通る直線の方程式を求めよ.
また,その交点を求めよ.
(1) (2)
(2) 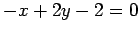 (3)
(3)  (4)
(4)
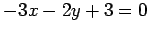
(1)
問 1.186 (直線の平面への射影)
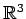 の直線
の直線
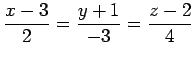 を平面
を平面 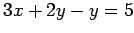 へ射影した直線を求めよ.
へ射影した直線を求めよ.
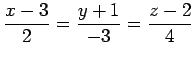 を平面
を平面
問 1.187 (総合)
3次元空間内の点  ,
,  ,
,  ,
,  を考える.
点
を考える.
点  から直線
から直線  に垂線を下ろしたときの足を
に垂線を下ろしたときの足を  とする.
とする.
 点
点 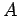 ,
,  ,
,  を通る平面を
を通る平面を 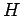 とする.
点
とする.
点  から平面
から平面 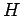 への垂線を
への垂線を 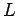 とする.
平面
とする.
平面 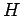 と 直線
と 直線 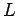 の交点を
の交点を  とする.
このとき,
とする.
このとき,
 ,
,
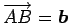 ,
,
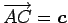 ,
,
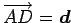 とおく.
次の問(1)-(14)に答えよ.
(1) ベクトル
とおく.
次の問(1)-(14)に答えよ.
(1) ベクトル  と
と 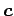 のノルムをそれぞれ求めよ.
(2) 内積
のノルムをそれぞれ求めよ.
(2) 内積
 を求めよ.
(3) 角
を求めよ.
(3) 角
 を示せ.
(4) ベクトル
を示せ.
(4) ベクトル  を正規化したベクトル
を正規化したベクトル  を示せ.
(5) ベクトル
を示せ.
(5) ベクトル 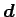 をベクトル
をベクトル  と
と 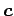 を用いて表せ.
(6) 点
を用いて表せ.
(6) 点  の座標を求めよ.
(7) 点
の座標を求めよ.
(7) 点  と直線
と直線  との距離を求めよ.
(8) 外積
との距離を求めよ.
(8) 外積
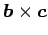 を求めよ.
(9) 平面
を求めよ.
(9) 平面 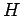 の法線ベクトル
の法線ベクトル 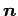 を求めよ.
(10) 平面
を求めよ.
(10) 平面 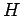 上の点
上の点  が満たす方程式を示せ.
(11) 直線
が満たす方程式を示せ.
(11) 直線 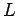 上の点の位置ベクトル
上の点の位置ベクトル  をパラメータ
をパラメータ 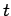 を用いて表せ.
(12) 直線
を用いて表せ.
(12) 直線 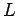 上の点
上の点  が満たす方程式を示せ.
(13) 点
が満たす方程式を示せ.
(13) 点  の座標を求めよ.
(14) 点
の座標を求めよ.
(14) 点  と平面
と平面 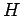 との距離を求めよ.
との距離を求めよ.
問 1.188 (総合)
 空間内に点
空間内に点  ,
,  ,
,  ,
,
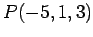 がある.
がある.
次の問(1)-(9)に答えよ. (1) 方向余弦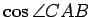 ,
,
 ,
,
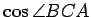 を求めよ.
(2) 直線
を求めよ.
(2) 直線  の単位方向ベクトルを求めよ.
(3) 直線
の単位方向ベクトルを求めよ.
(3) 直線  の方程式を成分表示で書け.
(4) 点
の方程式を成分表示で書け.
(4) 点  を直線
を直線  へ射影した点
へ射影した点  の座標を求めよ.
(5) 点
の座標を求めよ.
(5) 点  と直線
と直線  との距離を求めよ.
(6) 点
との距離を求めよ.
(6) 点 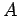 ,
,  ,
,  を通る平面
を通る平面 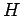 の法線ベクトルを求めよ.
(7) 平面
の法線ベクトルを求めよ.
(7) 平面 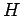 の方程式を成分表示で書け.
(8) 点
の方程式を成分表示で書け.
(8) 点  を平面
を平面 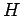 へ射影した点
へ射影した点  の座標を求めよ.
(9) 点
の座標を求めよ.
(9) 点  と平面
と平面 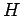 との距離を求めよ.
との距離を求めよ.
次の問(1)-(9)に答えよ. (1) 方向余弦
Kondo Koichi
 KONDO Koichi
KONDO Koichi
平成19年1月25日