5.10 2 項係数の拡張
定義 5.18 (階乗の拡張)
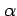 を実数とする.このとき
を実数とする.このとき 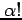 を
を
と定義する.
と定義する.
例 5.19 (階乗の具体例)
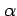 が自然数
が自然数 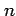 のとき
のとき
である.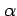 が自然数ではないとき
が自然数ではないとき
となり無限積で表わされる. 例えば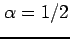 のときは
のときは
となる.
である.
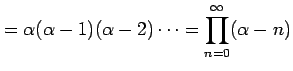 |
となり無限積で表わされる. 例えば
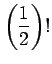 |
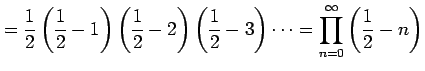 |
|
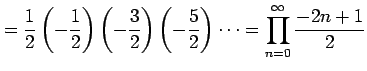 |
となる.
定義 5.20 (二項係数の拡張)
実数 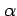 , 自然数
, 自然数 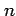 に対して
に対して
と定義する.
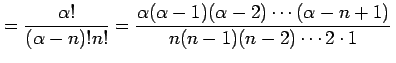 |
と定義する.
例 5.21 (二項係数の具体例)
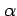 が自然数
が自然数  のときは
のときは
であり通常の二項係数と等しい.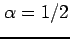 ,
, 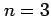 のとき
のとき
となる.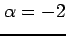 ,
, 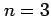 のとき
のとき
となる.
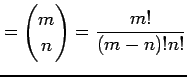 |
であり通常の二項係数と等しい.
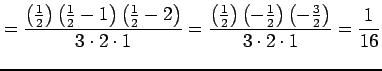 |
となる.
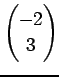 |
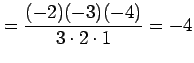 |
となる.
平成19年10月3日