6.7 有理関数の積分
有理関数
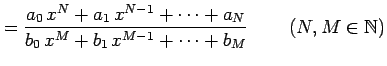 |
の不定積分
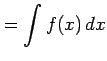 |
を考える. 任意の有理関数は積分可能である.
Step 1 (分子を分母で割る)
分子の次数 ![]() が分母の次数
が分母の次数 ![]() 以上のときは
まず割り算を行い,
以上のときは
まず割り算を行い,
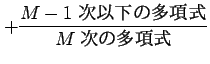 |
とする. このとき多項式の部分は必ず積分が可能である. よって以後では分子の次数
Step 2 (分母を因数分解する)
有理式を
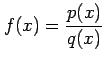 とする.
分母の多項式
とする.
分母の多項式 ![]() を実数の範囲で因数分解する.
このとき
を実数の範囲で因数分解する.
このとき
と表される.
Step 3 (部分分数分解する)
有理式
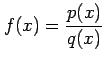 を
部分分数分解する.
すなわち
を
部分分数分解する.
すなわち
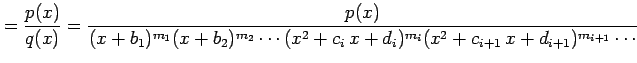 |
||
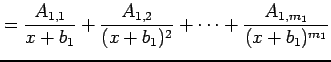 |
||
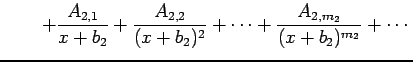 |
||
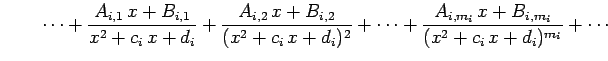 |
と変形する.
問 6.31 (部分分数分解)
任意の有理式
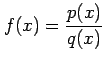
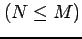 は
上式のように部分分数分解される.これを示せ.
は
上式のように部分分数分解される.これを示せ.
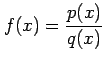
Step 4 (部分分数ごとに積分する)
部分分数ごとに積分を行う.
すなわち
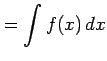 |
||
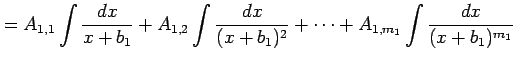 |
||
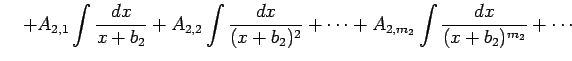 |
||
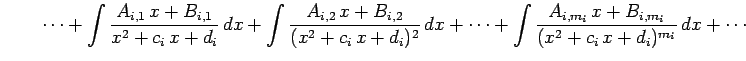 |
を計算する. それぞれの場合ごとに積分を考える.
分母の因子が ![]() 次式の場合
次式の場合
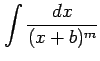 |
の積分を行なう.
Type 1: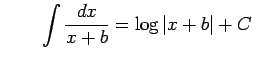 |
となる.
Type 2: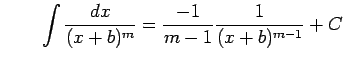 |
となる.
分母の因子が ![]() 次式の場合の積分を行なう.
次式の場合の積分を行なう.
![]() 次式の判別式が負であることに注意すると
次式の判別式が負であることに注意すると
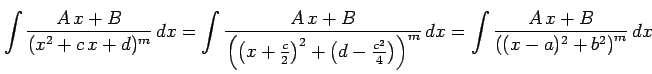 |
||
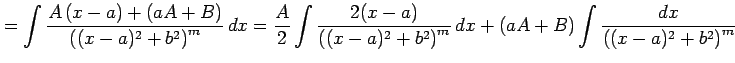 |
||
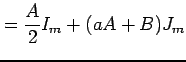 |
と表される. ここで
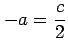 ,
,
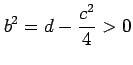 ,
, 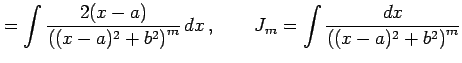 |
とおいた. 積分
| Type 3: |
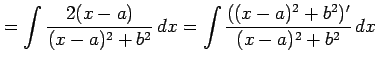 |
|
となり,
| Type 4: |
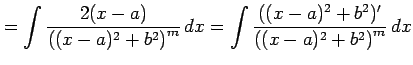 |
|
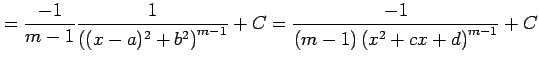 |
と求まる. 第二項目の積分
| Type 5: |
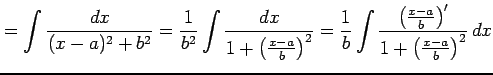 |
|
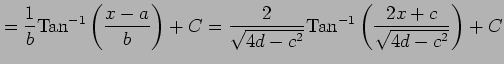 |
となる.
| Type 6: |
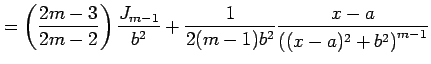 |
|
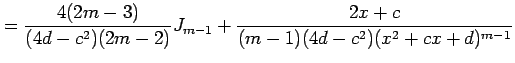 |
より
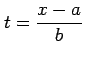 とおいて置換積分を用いると
とおいて置換積分を用いると
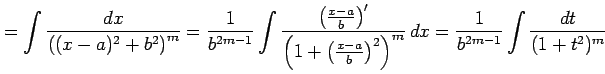 |
となる. 分子を変形すると
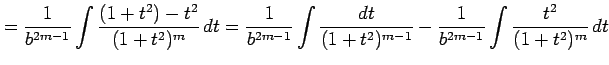 |
第 1 項は
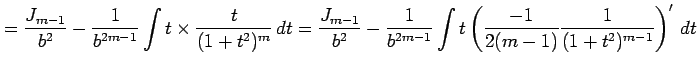 |
||
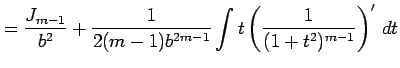 |
||
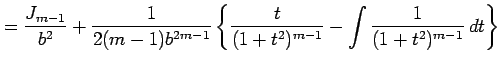 |
となる.残った積分も
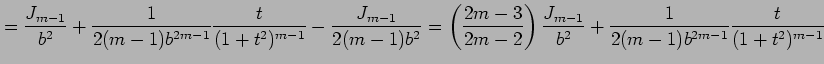 |
||
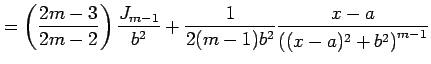 |
となり漸化式を得る.
例 6.32 (分子の次数を下げる)
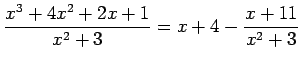 |
例 6.33 (分母の因数分解)
例 6.34 (部分分数展開の具体例)
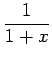 |
||
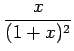 |
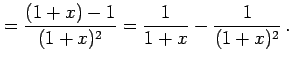 |
|
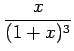 |
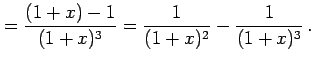 |
|
 |
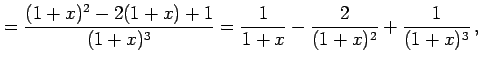 |
|
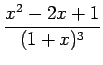 |
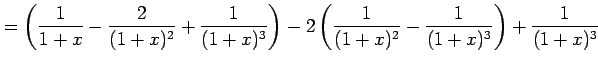 |
|
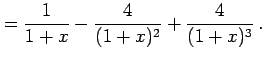 |
問 6.35 (部分分数展開の計算例)
部分分数分解として
とする. 係数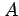 ,
, 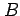 ,
, 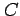 ,
, 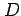 を定めよ.
を定めよ.
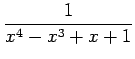 |
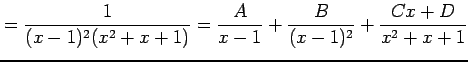 |
とする. 係数
問 6.36 (部分分数展開の計算例)
部分分数分解として
とする. 係数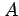 ,
, 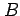 ,
, 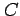 ,
, 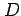 ,
, 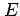 ,
, 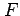 ,
, 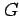 ,
, 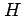 を定めよ.
を定めよ.
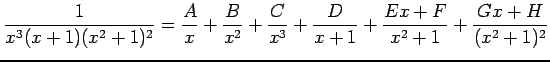 |
とする. 係数
例 6.37 (部分分数の積分の計算例)
Type 1:
Type 2:
Type 3:
Type 4:
Type 5:
Type 6: これはあとの例題で示す.
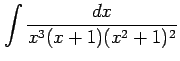 |
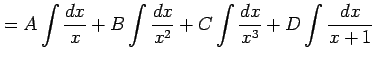 |
|
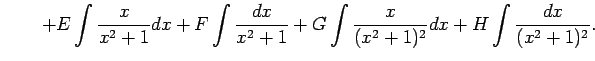 |
Type 1:
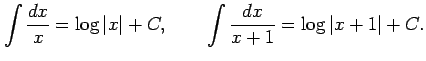 |
Type 2:
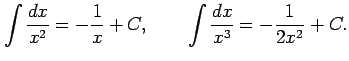 |
Type 3:
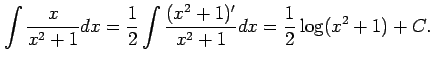 |
Type 4:
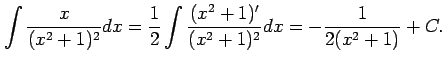 |
Type 5:
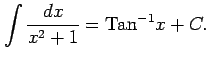 |
Type 6: これはあとの例題で示す.
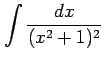 |
問 6.38 (有理式関数の不定積分)
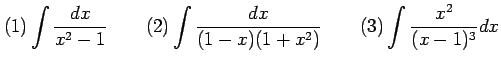 |
例 6.39 (有理式関数の不定積分の具体例)
(Type 1 のみ)
不定積分
を計算する. まず,部分分数分解する.
とおくと,
であり,これを解くと
となる.よって
を得る. これを積分して
を得る.
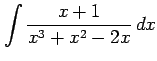 |
を計算する. まず,部分分数分解する.
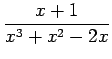 |
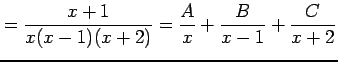 |
|
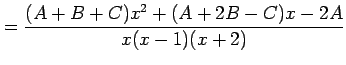 |
とおくと,
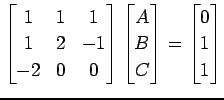 |
であり,これを解くと
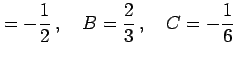 |
となる.よって
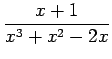 |
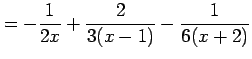 |
を得る. これを積分して
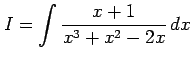 |
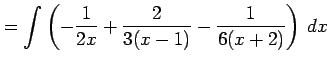 |
|
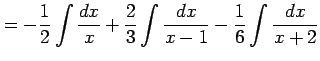 |
||
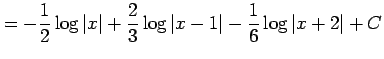 |
||
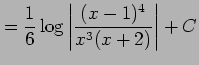 |
を得る.
例 6.40 (有理式関数の不定積分の具体例)
(Type 1, 3, 5)
不定積分
を計算する.まず, 部分分数分解として
とする. 通分して同じ次数でまとめると
となる.よって係数は
を満足しなければならない. これを解くと
となる. よって部分分数分解は
と表される. よって,
を得る.
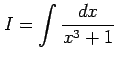 |
を計算する.まず, 部分分数分解として
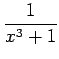 |
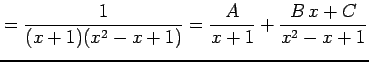 |
とする. 通分して同じ次数でまとめると
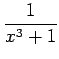 |
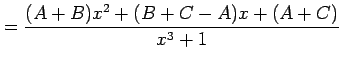 |
となる.よって係数は
 |
を満足しなければならない. これを解くと
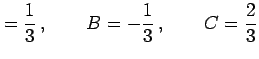 |
となる. よって部分分数分解は
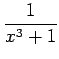 |
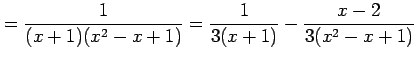 |
と表される. よって,
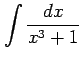 |
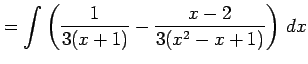 |
|
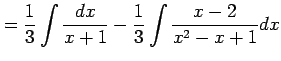 |
||
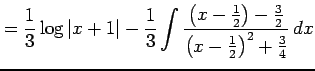 |
||
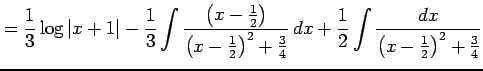 |
||
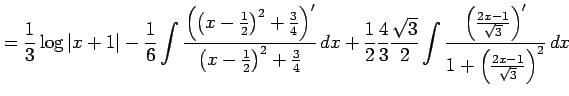 |
||
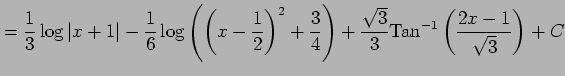 |
||
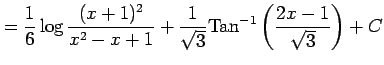 |
を得る.
例 6.41 (有理式関数の不定積分の具体例)
(Type 1, 3, 5)
不定積分
を計算する. まず
とおくと
より
が定まる.よって
となる.これより
を得る.
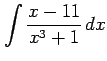 |
を計算する. まず
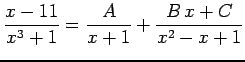 |
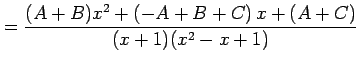 |
とおくと
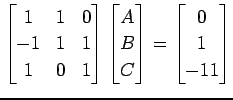 |
より
が定まる.よって
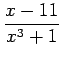 |
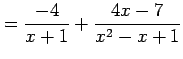 |
となる.これより
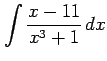 |
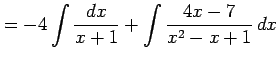 |
|
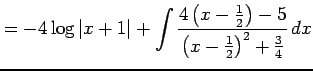 |
||
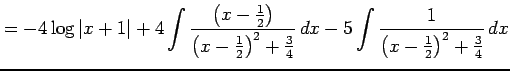 |
||
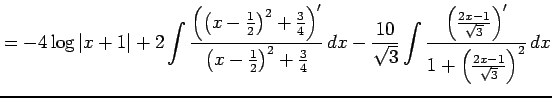 |
||
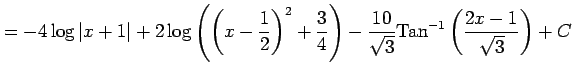 |
||
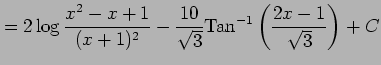 |
を得る.
例 6.42 (有理式関数の不定積分の具体例)
(Step1, Type 3, 5)
不定積分
を計算する. 分子の次数が分母の次数以上であるから, 分子を分母で割り
のように変形する. 多項式部分は積分される. 残るは有理式の積分である. これを計算すると
となる. よって
を得る.
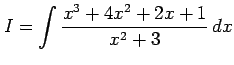 |
を計算する. 分子の次数が分母の次数以上であるから, 分子を分母で割り
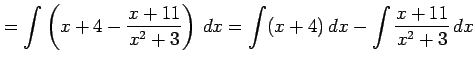 |
||
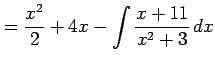 |
のように変形する. 多項式部分は積分される. 残るは有理式の積分である. これを計算すると
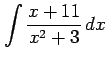 |
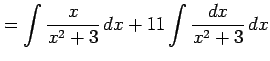 |
|
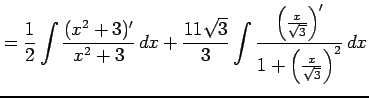 |
||
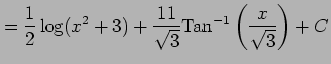 |
となる. よって
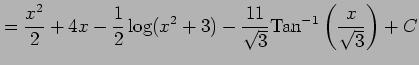 |
を得る.
例 6.43 (有理式関数の不定積分の具体例)
(Type 6)
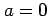 ,
, 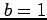 の場合の
の場合の 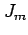 を求める.
を求める.
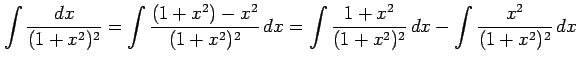 |
||
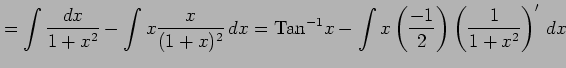 |
||
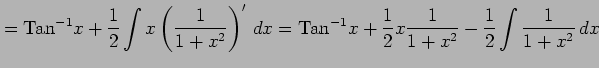 |
||
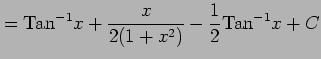 |
||
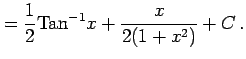 |
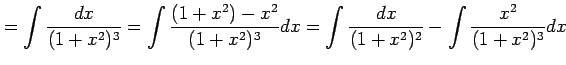 |
||
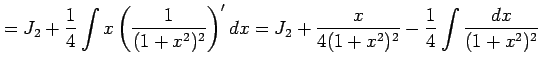 |
||
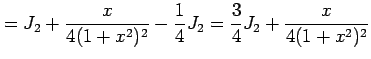 |
||
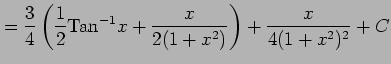 |
||
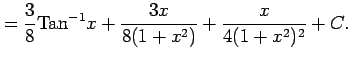 |
平成19年10月3日