6.8 1 次式の根号を含む関数の積分
定理 6.44 (根号を含む場合の計算)
関数  に根号
に根号
![$ \sqrt[n]{ax+b}$](img2568.png)
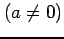 を含む場合の
不定積分を考える.
変数変換
を含む場合の
不定積分を考える.
変数変換
とおき置換積分法で求積する. 両辺を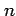 乗すると
乗すると
を得る.またこれより
が成り立つ.よって の不定積分は
の不定積分は
より求められる.
とおき置換積分法で求積する. 両辺を
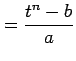 |
を得る.またこれより
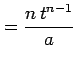 |
が成り立つ.よって
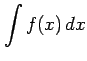 |
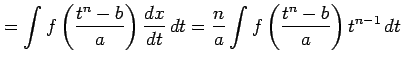 |
より求められる.
例 6.45 (根号を含む場合の計算例)
不定積分
を考える.まず
とおく.これより
となる.よって置換積分法より
を得る.
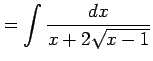 |
を考える.まず
とおく.これより
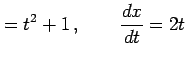 |
となる.よって置換積分法より
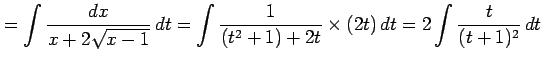 |
||
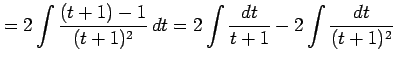 |
||
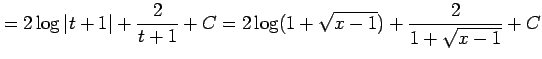 |
を得る.
例 6.46 (根号を含む不定積分)
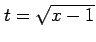 とおいて置換積分を行う:
とおいて置換積分を行う:
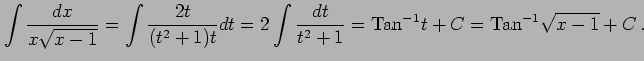 |
例 6.47 (根号を含む不定積分)
![$ t=\sqrt[3]{x}$](img2582.png) ,
, 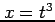 ,
,
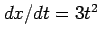 とおき,
さらに
とおき,
さらに
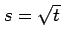 ,
, 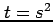 ,
, 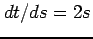 とおいて置換積分する:
とおいて置換積分する:
![$\displaystyle \int\frac{\sqrt{x}}{1+\sqrt[3]{x}}dx= \int\frac{(\sqrt{t})^33t^2}...
...^2(\sqrt{t})^3}{1+t}dt= 3\int\frac{s^4s^32s}{1+s^2}ds= 6\int\frac{s^8}{1+s^2}ds$](img2588.png) |
||
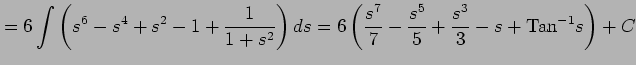 |
||
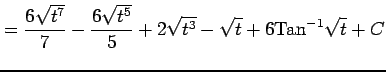 |
||
![$\displaystyle = \frac{6x\sqrt[6]{x}}{7}-\frac{6\sqrt[6]{x^5}}{5}+2\sqrt{x}-\sqrt[6]{x}+6\mathrm{Tan}^{-1}\sqrt[6]{x}+C,.$](img2591.png) |
平成19年10月3日