6.9 2 次式の根号を含む関数の積分
定理 6.48 (根号を含む場合の計算)
関数  に
に
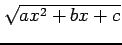
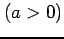 を
含む場合を考える.
このときまず
を
含む場合を考える.
このときまず
とおく.両辺を二乗すれば
を得る.これより
となる. このとき不定積分は
により求まる.
とおく.両辺を二乗すれば
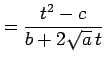 |
を得る.これより
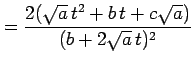 |
となる. このとき不定積分は
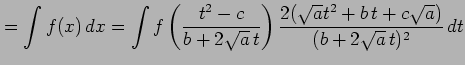 |
により求まる.
例 6.49 (根号を含む場合の計算例)
不定積分
を考える. 変数変換
とおく.両辺を二乗すれば
を得る.これより
となる. よって不定積分は
と求まる.またこの結果は
とも表される.
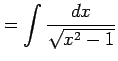 |
を考える. 変数変換
とおく.両辺を二乗すれば
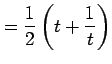 |
を得る.これより
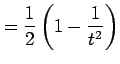 |
となる. よって不定積分は
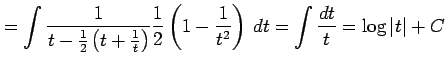 |
||
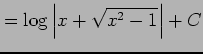 |
と求まる.またこの結果は
とも表される.
問 6.50 (根号を含む場合の不定積分)
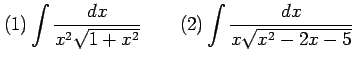 |
定理 6.51 (根号を含む場合の計算)
関数  に
に
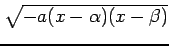
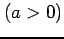 を
含む場合を考える.
このときまず
を
含む場合を考える.
このときまず
と変形し,
とおく.このとき,
となる. このとき不定積分は
により求まる.
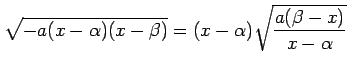 |
と変形し,
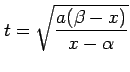 |
とおく.このとき,
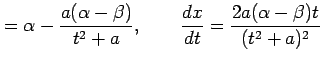 |
となる. このとき不定積分は
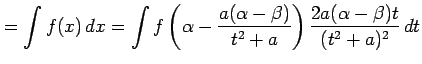 |
により求まる.
例 6.52 (根号を含む場合の計算例)
不定積分
を求める. 変数変換
とおく.このとき
である.よって
を得る.
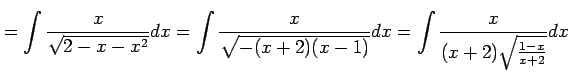 |
を求める. 変数変換
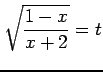 |
とおく.このとき
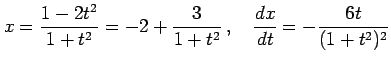 |
である.よって
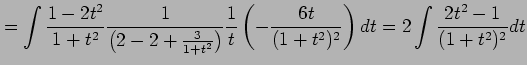 |
||
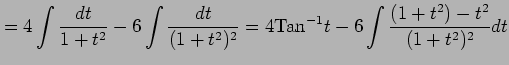 |
||
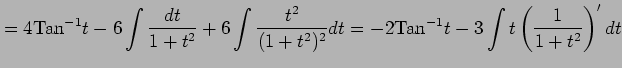 |
||
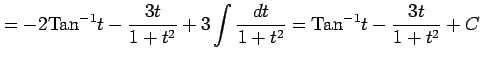 |
||
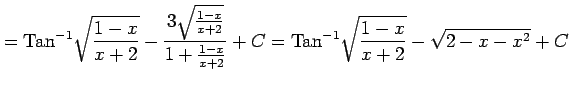 |
を得る.
平成19年10月3日