6.10 三角関数の有理式の積分
三角関数の有理式
![]() の不定積分を考える.
まず変数変換として
の不定積分を考える.
まず変数変換として
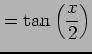 |
とおく. このとき
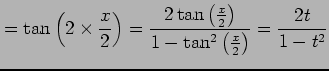 |
となる. 同様にして
 |
||
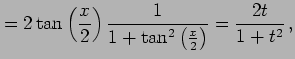 |
||
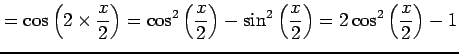 |
||
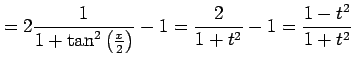 |
となる.次に
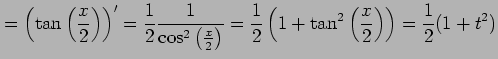 |
となるので
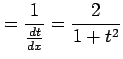 |
を得る. よって不定積分は
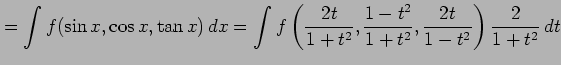 |
により求められる.
例 6.53 (三角関数を含む場合の積分の計算例)
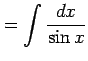 |
||
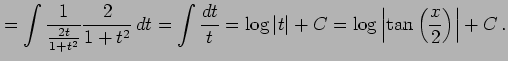 |
例 6.54 (三角関数を含む場合の積分の計算例)
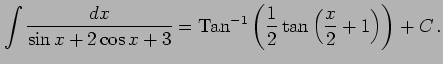 |
平成19年10月3日
6.10 三角関数の有理式の積分
三角関数の有理式
の不定積分を考える. まず変数変換として
とおく. このとき
となる. 同様にして
となる.次にを
で微分すると
となるので
を得る. よって不定積分は
により求められる.
例 6.53 (三角関数を含む場合の積分の計算例)
例 6.54 (三角関数を含む場合の積分の計算例)
平成19年10月3日