6.13 定積分の性質
定理 6.63 (定積分の性質)
定積分は次の性質をもつ:
- (1)
-
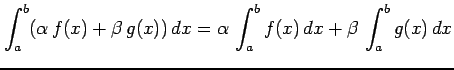 .
.
- (2)
-
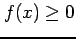
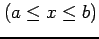 のとき
のとき
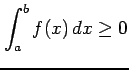 .
.
- (3)
-
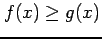
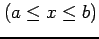 のとき
のとき
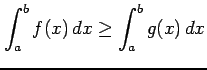 .
.
- (4)
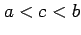 のとき
のとき
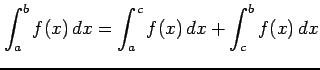 .
.
- (5)
-
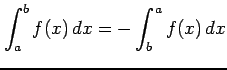 .
.
- (6)
-
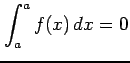 .
.
- (7)
-
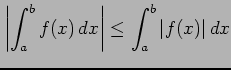
定理 6.64 (定積分の性質)
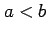 に対して
に対して
をみたす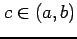 が存在する.
が存在する.
が成り立つ.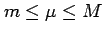 ,
,
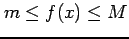 より中間値の定理より
より中間値の定理より
をみたす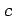 が存在する.
が存在する.
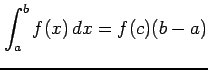 |
をみたす
(証明)
![]() のとき
のとき
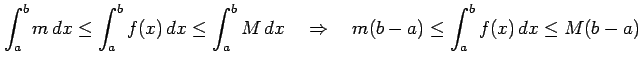 |
||
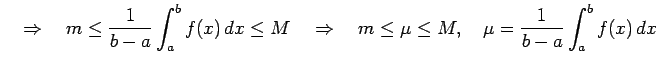 |
が成り立つ.
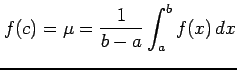 |
をみたす
定理 6.65 (中間値の定理)
関数  が区間
が区間 ![$ [a,b]$](img2663.png) で連続であるとき,
で連続であるとき,
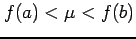 をみたす任意の
をみたす任意の 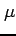 に対して,
に対して,
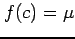 ,
, 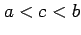 をみたす
をみたす 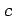 が存在する.
が存在する.
平成19年10月3日