6.12 定積分
定義 6.58 (定積分)
関数  は有限区間
は有限区間 ![$ [a,b]$](img2663.png) で連続とする.
区間
で連続とする.
区間 ![$ [a,b]$](img2663.png) を
を
のように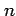 個の領域に分割する.
小区間
個の領域に分割する.
小区間 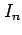 の最小幅を
の最小幅を
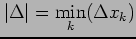 とする.
面積
とする.
面積
が分割の選び方に無関係に,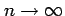 ,
,
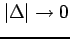 のとき極限をもつならば,
この極限を
のとき極限をもつならば,
この極限を
と書き, 関数 の
の 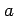 から
から 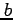 までの
定積分(definite integral)という.
このとき
までの
定積分(definite integral)という.
このとき
 は積分可能であるという.
区間
は積分可能であるという.
区間 ![$ [a,b]$](img2663.png) を積分区間という.
を積分区間という.
のように
![$\displaystyle = \sum_{k=1}^{n} f(\xi_{k})\Delta x_{k}\,,\quad \xi_{k}\in I_{k}=[x_{k}, x_{k-1}]\,,\quad \Delta x_{k}=x_{k}-x_{k-1}$](img2666.png) |
が分割の選び方に無関係に,
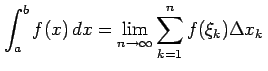 |
と書き, 関数
注意 6.59 (定積分の意味)
区間 ![$ [a,b]$](img2663.png) において
において 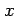 軸と
軸と 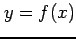 とで囲まれた領域の
符合付き面積である.
とで囲まれた領域の
符合付き面積である.
例 6.60 (定積分の具体例)
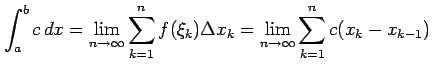 |
||
定理 6.61 (積分可能)
すべての分割 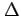 に対して
に対して
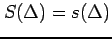 であるとき
積分可能である.
ここで
であるとき
積分可能である.
ここで 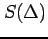 ,
, 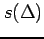 は
は
である.
が成り立つ.
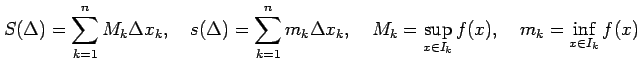 |
である.
(証明)
分割 ![]() の各領域をさらに分割した分割を細分といい,
の各領域をさらに分割した分割を細分といい,
![]() とおくことにする.
このとき明らかに
とおくことにする.
このとき明らかに
が成り立つ.
定理 6.62 (積分可能)
関数  が区間
が区間 ![$ [a,b]$](img2663.png) で連続ならば積分可能である.
で連続ならば積分可能である.
が成り立つ.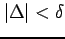 のとき
のとき
(証明)
区間 ![]() で
で ![]() が連続であれば,
が連続であれば,
![]() は
は ![]() で一様連続である.つまり,
で一様連続である.つまり,
![]() に対して,
に対して,
が成り立つ.
平成19年10月3日