2.25 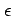 -
-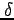 論法
論法
定義 2.88 (関数の極限)
関数  が次の条件(i)をみたすとき,
が次の条件(i)をみたすとき,
と表記する.
をみたす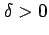 が存在する.
が存在する.
と表記する.
(i)
![]() に対して
に対して
をみたす
定義 2.89 (関数の連続)
関数 が点
が点 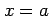 で連続であるとは,
で連続であるとは,
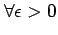 に対して
に対して
をみたす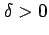 が存在するときをいう.
が存在するときをいう.
をみたす
定義 2.90 (一様連続)
関数  が定義域
が定義域 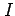 において一様連続であるとは,
において一様連続であるとは,
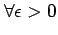 に対して
に対して
をみたす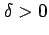 が存在するときをいう.
が存在するときをいう.
をみたす
定理 2.91 (連続と一様連続)
関数  が区間
が区間 ![$ I=[a,b]$](img555.png) 連続なとき,
連続なとき,
 は
は 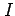 において一様連続である.
において一様連続である.
注意 2.92 (連続と一様連続)
開区間 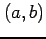 において連続なときは一様連続になるとは限らない.
において連続なときは一様連続になるとは限らない.
平成19年10月3日