4.3 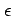 論法
論法
定義 4.9 (数列の極限)
数列 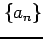 と実数
と実数 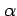 が次の条件(i)をみたすとき
が次の条件(i)をみたすとき
と表記する.
と表記する.
(i) 任意の正の数 ![]() に対して,
に対して,
![]() のとき
のとき
![]() をみたす
自然数
をみたす
自然数 ![]() が存在する.
が存在する.
例 4.10 (数列の極限の証明の例)
数列
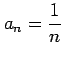 の極限
の極限
の証明をする. 任意の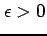 に対して自然数
に対して自然数 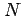 を
を
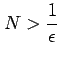 となるように選ぶ.
このとき
となるように選ぶ.
このとき 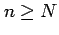 ならば
ならば
となるので
より
を得る.
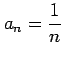 の極限
の極限
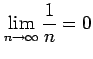 |
の証明をする. 任意の
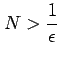 となるように選ぶ.
このとき
となるように選ぶ.
このとき 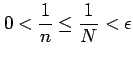 |
となるので
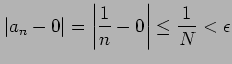 |
より
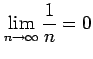 |
を得る.
問 4.11 (数列の極限)
数列 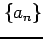 が
が
をみたすとき
となることを示せ.
をみたすとき
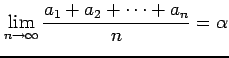 |
となることを示せ.
平成19年10月3日