4.5 数列の極限に関する定理
注意 4.16 (数列の速さ)
注意 4.17 (不定形)
四則演算と極限の操作は一般に交換可能ではない.
極限操作をし不定形
と呼ばれる形になるときは注意が必要である. このままではまだ有限確定とも無限確定とも分からない. もしこの形のになるときは式変形をした後に極限操作を行う. 極限が有限確定または無限確定
するように計算方法を工夫する.
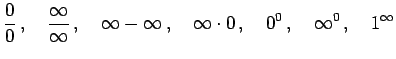 |
と呼ばれる形になるときは注意が必要である. このままではまだ有限確定とも無限確定とも分からない. もしこの形のになるときは式変形をした後に極限操作を行う. 極限が有限確定または無限確定
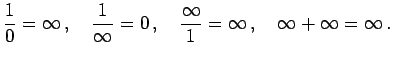 |
するように計算方法を工夫する.
次の定理はある条件の下では方程式の項の移行が可能であることを意味する.
定理 4.18 (数列の極限に関する定理)
一般には極限操作と四則演算は交換可能ではないが ある条件の下では可能である. 次の定理はそれを保証する.
定理 4.19 (数列の極限に関する定理)
数列 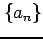 ,
, 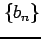 に関して極限
に関して極限
が存在するとき,次の関係式が成り立つ:
ただし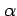 ,
, 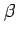 は定数とする.
は定数とする.
が存在するとき,次の関係式が成り立つ:
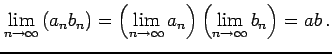 |
||
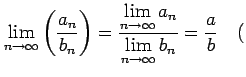 |
ただし
定理 4.20 (はさみうちの定理)
数列 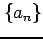 ,
, 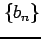 ,
, 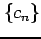 が
が
をみたすとき,
ならば,
が成り立つ.
をみたすとき,
ならば,
が成り立つ.
平成19年10月3日