4.16 交項級数
定義 4.64 (交項級数)
級数
を交項級数(alternative term series)と呼ぶ.
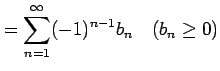 |
を交項級数(alternative term series)と呼ぶ.
定理 4.65 (交項級数の収束定理)
交項級数
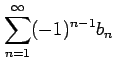 は
次の条件をみたすとき収束する:
は
次の条件をみたすとき収束する:
と書ける.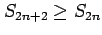 となるので,
数列
となるので,
数列
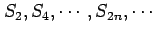 は正項級数でかつ単調増加となる.
さらには
は正項級数でかつ単調増加となる.
さらには 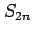 は
は
とも書ける.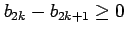 ,
,
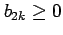 であるから,
であるから,
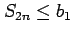 となる.よって
となる.よって 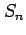 は
は
をみたす.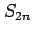 は有界な単調増加数列である.
よって
は有界な単調増加数列である.
よって 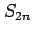 は極限
は極限
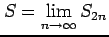 が存在する.
次に
が存在する.
次に 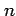 が奇数にる場合を考える.
が奇数にる場合を考える.
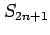 の極限は
の極限は
と得られる.以上で証明終了.
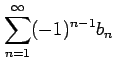 は
次の条件をみたすとき収束する:
は
次の条件をみたすとき収束する:
- (i)
-
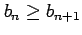 .
.
- (ii)
-
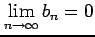 .
.
(証明)![]() が偶数のときの有限部分和は
が偶数のときの有限部分和は
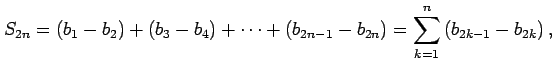 |
||
と書ける.
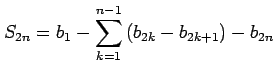 |
とも書ける.
をみたす.
と得られる.以上で証明終了.
例 4.66 (交項級数の収束定理の具体例)
級数
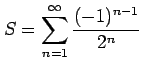 は
収束する.
なぜなら
は
収束する.
なぜなら
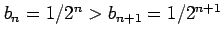 であり,
であり,
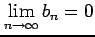 であるから,
定理より級数は収束する.
であるから,
定理より級数は収束する.
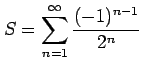 は
収束する.
なぜなら
は
収束する.
なぜなら
例 4.67 (交項級数の収束定理の具体例)
級数
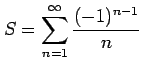 は
収束する.
なぜなら
は
収束する.
なぜなら
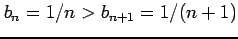 であり,
であり,
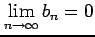 であるから,
定理より級数は収束する.
であるから,
定理より級数は収束する.
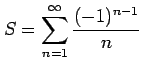 は
収束する.
なぜなら
は
収束する.
なぜなら
平成19年10月3日