5.7 対数関数のマクローリン級数
例 5.15 (対数関数のテイラー級数)
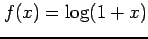 とおく.
導関数を計算すると
とおく.
導関数を計算すると
となる.一般的には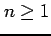 に対して
に対して
と表わされる. 点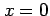 における微分係数は
における微分係数は
となる. よってテーラー級数は
と得られる. 収束半径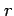 を求める.
を求める.
とおくと,
と得られる.
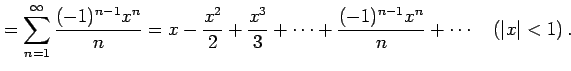 |
(導出)
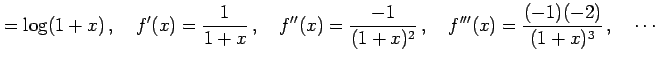 |
となる.一般的には
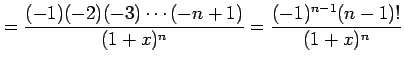 |
と表わされる. 点
となる. よってテーラー級数は
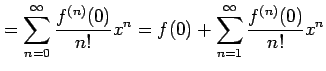 |
||
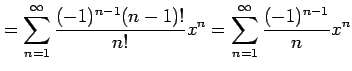 |
と得られる. 収束半径
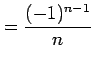 |
とおくと,
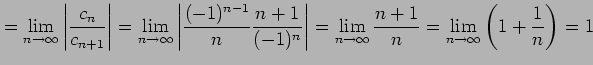 |
と得られる.
平成19年10月3日