2.8 高階偏微分
関数 ![]() の 1 階偏導関数
の 1 階偏導関数 ![]() ,
, ![]() は
は
![]() ,
, ![]() に関する 2 変数関数であるから,
さらに
に関する 2 変数関数であるから,
さらに ![]() または
または ![]() に関して偏微分することができる.
このとき
に関して偏微分することができる.
このとき
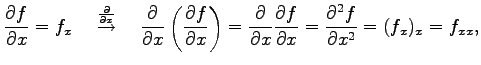 |
||
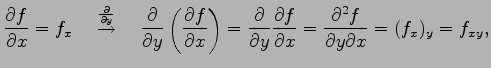 |
||
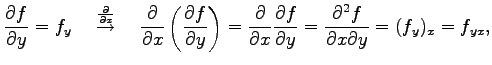 |
||
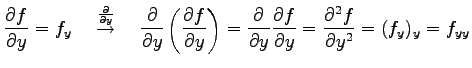 |
と表記する. これを2 階偏導関数という. さらに偏微分すると
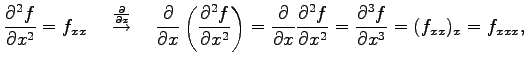 |
||
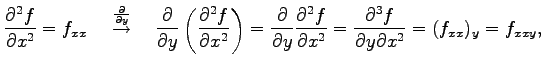 |
||
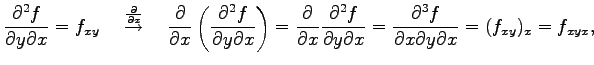 |
||
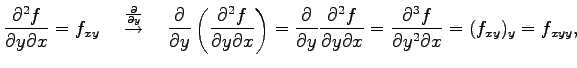 |
||
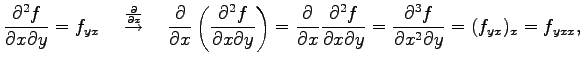 |
||
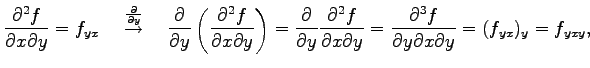 |
||
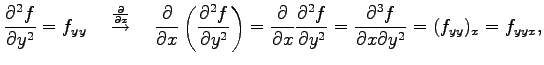 |
||
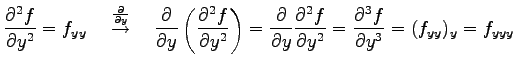 |
と表記し3 階偏導関数という. さらに偏微分を繰り返して
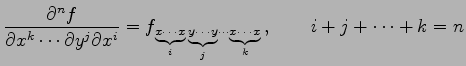 |
と表記し,
例 2.35 (高階導関数)
関数
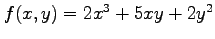 の高階偏導関数は,
の高階偏導関数は,
となり,さらに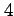 階以上の偏導関数はすべて 0 となる.
ここで,この関数の場合は
階以上の偏導関数はすべて 0 となる.
ここで,この関数の場合は
となることに注意する.
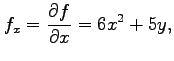 |
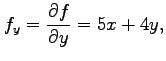 |
|||
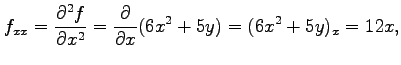 |
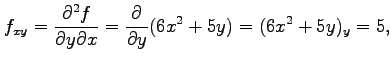 |
|||
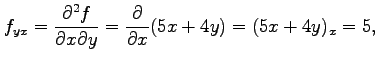 |
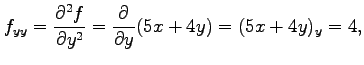 |
|||
 |
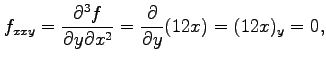 |
|||
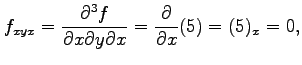 |
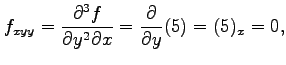 |
|||
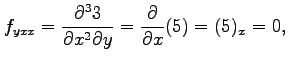 |
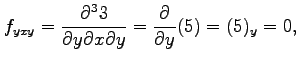 |
|||
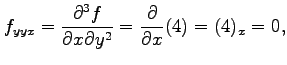 |
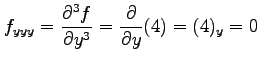 |
となり,さらに
となることに注意する.
注意 2.36 (偏微分の可換性)
一般には偏微分は交換可能ではない:
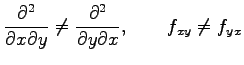 |
定理 2.37 (偏微分の可換性)
関数 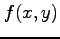 において,
において,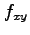 ,
, 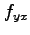 が存在し,
かつこれらが連続関数であるとき,
が存在し,
かつこれらが連続関数であるとき,
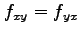 が成り立つ.
(注意)逆は成り立たない.
が成り立つ.
(注意)逆は成り立たない.
注意 2.38 (偏微分の可換性)
偏微分が可換となる十分条件は他にも色々あるが,
実用上は上の定理が一番有用である.
ほとんどの普通の関数はこの定理の十分条件をみたし,
偏微分が 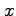 ,
, 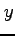 について可換となる.
について可換となる.
問 2.39 (偏導関数)
次の関数の高階偏導関数を計算し,
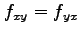 ,
,
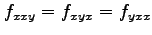 ,
,
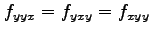 となることを確認せよ.
となることを確認せよ.
(1)
![]() (2)
(2)
![]()
(3)
![]() (4)
(4)
![]() (5)
(5)
![]()
(6)
![]() (7)
(7)
![]()
平成20年2月2日