2.9 演習問題 〜 偏微分
問 2.40 (1 階偏導関数)
次の関数の 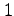 階偏導関数を全て求めよ.
階偏導関数を全て求めよ.
(1)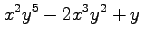 (2)
(2)
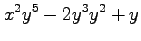 (3)
(3)
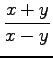 (4)
(4)
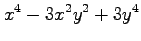
(5)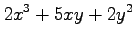 (6)
(6)
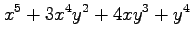 (7)
(7)
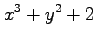 (8)
(8)
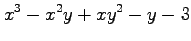
(9)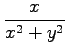 (10)
(10)
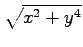 (11)
(11)
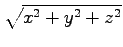 (12)
(12)
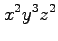 (13)
(13)
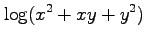
(14)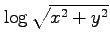 (15)
(15)
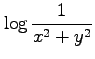 (16)
(16)
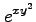 (17)
(17)
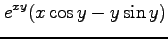 (18)
(18)
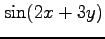
(19)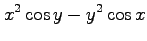 (20)
(20)
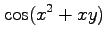 (21)
(21)
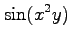 (22)
(22)
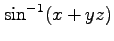 (23)
(23)
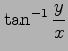
(24)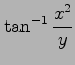 (25)
(25)
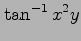
(1)
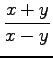 (4)
(4)
(5)
(9)
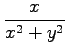 (10)
(10)
(14)
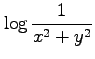 (16)
(16)
(19)
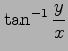
(24)
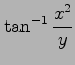 (25)
(25)
問 2.41 (2 階偏導関数)
次の関数の 1 階, 2 階偏導関数を全て求めよ.
(1)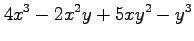 (2)
(2)
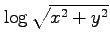 (3)
(3)
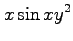 (4)
(4)
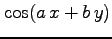
(5)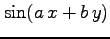 (6)
(6)
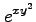
(7)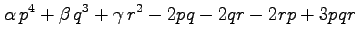 (
(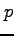 ,
, 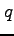 ,
, 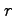 について)
について)
(1)
(5)
(7)
問 2.42 (3 階偏導関数)
次の関数の 1 階, 2 階, 3 階偏導関数を全て求めよ.
(1)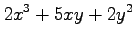 (2)
(2)
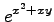
(1)
問 2.43 (偏微分)
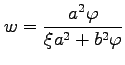 であるとき
であるとき
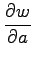 ,
,
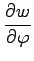 ,
,
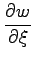 ,
,
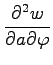 ,
,
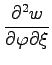 を求めよ.
を求めよ.
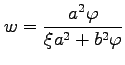 であるとき
であるとき
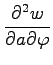 ,
,
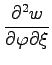 を求めよ.
を求めよ.
平成20年2月2日