2.19 2 変数関数 と 2 変数関数の合成関数の微分
定理 2.83 (合成関数の微分)
2 変数関数 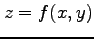 と 2 変数関数
と 2 変数関数
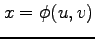 ,
,
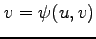 の
合成関数
の
合成関数
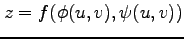 の偏微分は
の偏微分は
で与えられる.代入も含めて書くと
と表される.
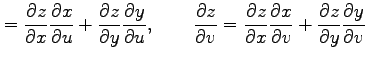 |
で与えられる.代入も含めて書くと
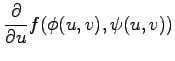 |
||
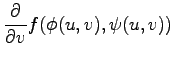 |
と表される.
例 2.84 (合成関数の微分の具体例)
関数
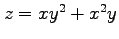 と関数
と関数 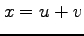 ,
, 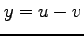 の
合成関数の偏導関数を求める.まず,
の
合成関数の偏導関数を求める.まず,
より,
を得る.
より,
を得る.
例 2.85 (合成関数の微分の具体例)
関数
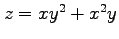 と関数
と関数
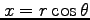 ,
,
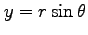 の
合成関数の偏導関数を求める.まず,
の
合成関数の偏導関数を求める.まず,
より,
を得る.
より,
を得る.
平成20年2月2日