2.27 3 次元空間の極座標
定義 2.118 (極座標)
3 次元空間において,
直交座標 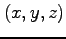 から
極座標(polar coordinates)
から
極座標(polar coordinates)
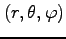 への
座標変換は
への
座標変換は
で与えられる.
で与えられる.
注意 2.119 (極座標)
極座標
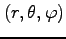 から
直交座標
から
直交座標 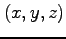 への座標変換は
への座標変換は
と表される.
 |
と表される.
![\includegraphics[width=0.5\textwidth]{polar3.eps}](img981.png)
例 2.120 (極座標のヤコビアン)
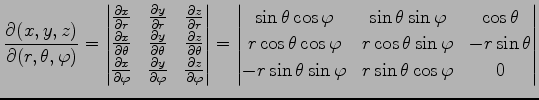 |
||
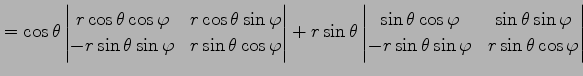 |
||
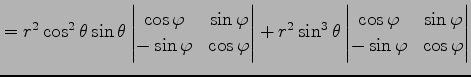 |
||
例 2.121 (極座標における偏微分作用素の変換)
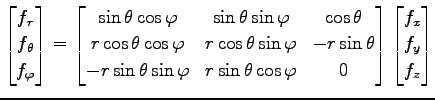 |
例 2.122 (極座標における偏微分作用素の変換)
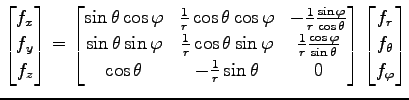 |
例 2.123 (極座標におけるラプラシアン)
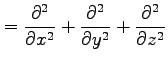 |
||
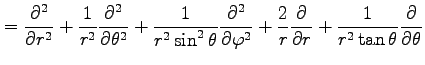 |
平成20年2月2日