2.41 演習問題 〜 陰関数,接線,接平面
問 2.179 (陰関数)
次の条件から定まる陰関数 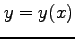 について
について 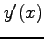 を求めよ.
を求めよ.
(1)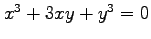 (2)
(2)
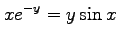 (3)
(3)
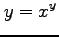 (4)
(4)
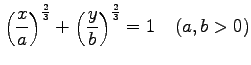
(5)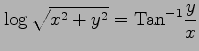 (6)
(6)
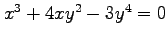 (7)
(7)
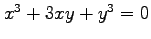 (8)
(8)
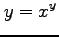
(9)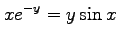 (10)
(10)
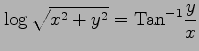
(1)
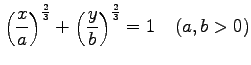
(5)
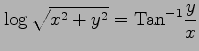 (6)
(6)
(9)
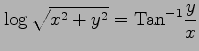
問 2.180 (陰関数)
次の条件から定まる陰関数 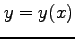 について
について
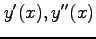 を求めよ.
を求めよ.
(1)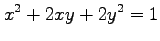 (2)
(2)
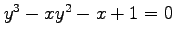 (3)
(3)
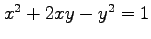
(1)
問 2.181 (陰関数)
次の条件から定まる陰関数 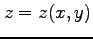 について
について
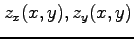 を求めよ.
を求めよ.
(1)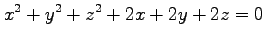 (2)
(2)
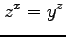 (3)
(3)
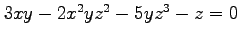
(4)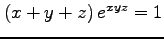
(1)
(4)
問 2.182 (陰関数)
次の条件から定まる陰関数 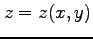 について
について
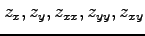 を求めよ.
を求めよ.
(1)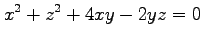 (2)
(2) 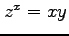
(1)
問 2.183 (陰関数の接線とテイラー展開)
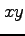 平面内の曲線
平面内の曲線 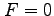 とこの曲線上の点
とこの曲線上の点 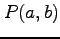 を考える.
を考える.
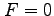 で定義される陰関数を
で定義される陰関数を 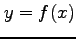 とおく.
点
とおく.
点 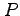 における曲線
における曲線 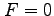 の接線の方程式を求めよ.
また,関数
の接線の方程式を求めよ.
また,関数 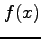 を
を 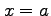 まわりでテイラー展開し 1 次近似せよ.
まわりでテイラー展開し 1 次近似せよ.
(1)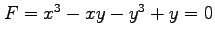 ,
, 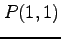
(2)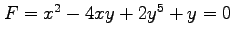 ,
, 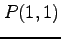
(3)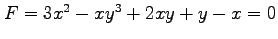 ,
, 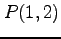
(1)
(2)
(3)
問 2.184 (接線)
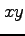 平面内の曲線
平面内の曲線 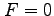 の点
の点 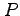 における接線の方程式を求めよ.
における接線の方程式を求めよ.
(1)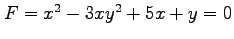 ,
, 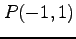 (2)
(2)
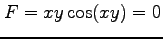 ,
,
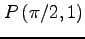
(3)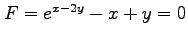 ,
, 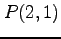
(1)
(3)
問 2.185 (陰関数の接平面とテイラー展開)
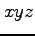 空間内の曲面
空間内の曲面 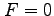 とこの曲面上の点
とこの曲面上の点 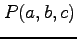 を考える.
を考える.
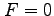 で定義される陰関数を
で定義される陰関数を 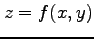 とおく.
点
とおく.
点 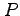 における曲面
における曲面 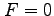 の接平面の方程式を求めよ.
また,関数
の接平面の方程式を求めよ.
また,関数 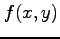 を点
を点 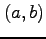 まわりで
まわりで 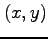 について
テイラー展開し 1 次近似
について
テイラー展開し 1 次近似
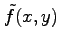 を求めよ.
を求めよ.
(1)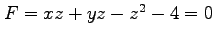 ,
, 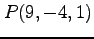
(2)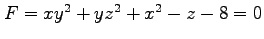 ,
, 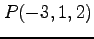
(1)
(2)
問 2.186 (接平面)
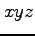 空間内の曲面
空間内の曲面 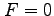 の点
の点 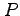 における接平面の方程式をそれぞれ求めよ.
における接平面の方程式をそれぞれ求めよ.
(1)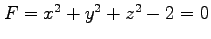 ,
,
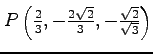
(2)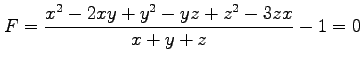 ,
,
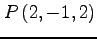
(3)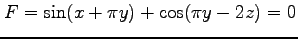 ,
,
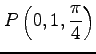
(1)
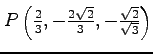
(2)
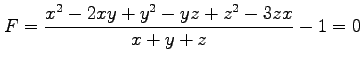 ,
,
(3)
平成20年2月2日