3.12 演習問題 〜 多重積分の積分変数の変換
問 3.56 (積分変数の変換)
多重積分
を求める.次の問に答えよ.
(1) 領域 を図示せよ.
(2)
領域
を図示せよ.
(2)
領域  と
領域
と
領域
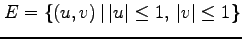 が等価となるように座標変換
が等価となるように座標変換
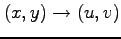 を定めよ.
(3) ヤコビアン
を定めよ.
(3) ヤコビアン
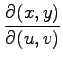 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分 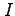 を求めよ.
を求めよ.
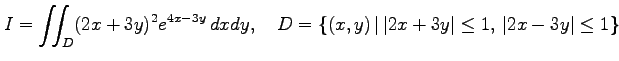 |
を求める.次の問に答えよ.
(1) 領域
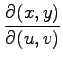 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分
問 3.57 (積分変数の変換)
多重積分
を求める.次の問に答えよ.
(1) 領域 を図示せよ.
(2)
座標変換
を図示せよ.
(2)
座標変換
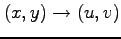 ;
;
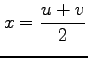 ,
,
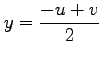 を行なう.
領域
を行なう.
領域  と等価な
と等価な 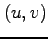 に関する
領域
に関する
領域 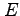 を求め,さらに図示せよ.
(3)
ヤコビアン
を求め,さらに図示せよ.
(3)
ヤコビアン
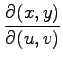 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分 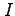 を求めよ.
を求めよ.
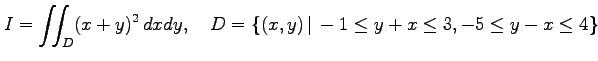 |
を求める.次の問に答えよ.
(1) 領域
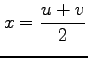 ,
,
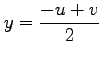 を行なう.
領域
を行なう.
領域 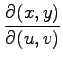 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分
問 3.58 (積分変数の変換)
多重積分
を求める.次の問に答えよ.
(1) 領域 を図示せよ.
(2) 座標変換
を図示せよ.
(2) 座標変換
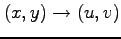 ;
;
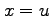 ,
,
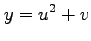 を行なう.
領域
を行なう.
領域  と等価な
と等価な 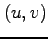 に関する領域
に関する領域 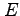 を求め,さらに図示せよ.
(3) ヤコビアン
を求め,さらに図示せよ.
(3) ヤコビアン
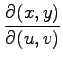 を
求めよ.
(4) 多重積分
を
求めよ.
(4) 多重積分 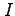 を求めよ.
を求めよ.
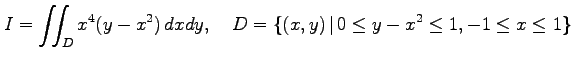 |
を求める.次の問に答えよ.
(1) 領域
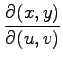 を
求めよ.
(4) 多重積分
を
求めよ.
(4) 多重積分
問 3.59 (積分変数の変換)
多重積分
を求める.次の問に答えよ.
(1) 領域 を図示せよ.
(2) 座標変換
を図示せよ.
(2) 座標変換
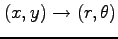 ;
;
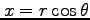 ,
,
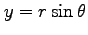 を行なう.
領域
を行なう.
領域  と等価な
と等価な
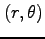 に関する
領域
に関する
領域 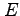 を求め,さらに図示せよ.
(3) ヤコビアン
を求め,さらに図示せよ.
(3) ヤコビアン
 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分 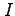 を求めよ.
を求めよ.
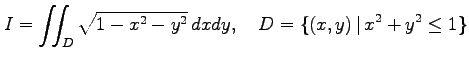 |
を求める.次の問に答えよ.
(1) 領域
 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分
問 3.60 (積分変数の変換)
多重積分
を求める.次の問に答えよ.
(1) 領域 を図示せよ.
(2) 座標変換
を図示せよ.
(2) 座標変換
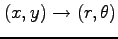 ;
;
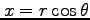 ,
,
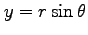 を行なう.
領域
を行なう.
領域  と等価な
と等価な
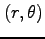 に関する
領域
に関する
領域 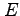 を求め,さらに図示せよ.
(3) ヤコビアン
を求め,さらに図示せよ.
(3) ヤコビアン
 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分 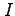 を求めよ.
を求めよ.
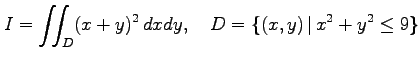 |
を求める.次の問に答えよ.
(1) 領域
 を求めよ.
(4) 多重積分
を求めよ.
(4) 多重積分
問 3.61 (積分変数の変換)
多重積分
を求める.次の問に答えよ.
(1) 座標変換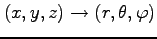 ;
;
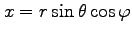 ,
,
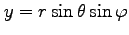 ,
,
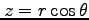 を行なう.
領域
を行なう.
領域  と等価な
と等価な
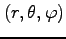 に関する
領域
に関する
領域 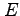 を求めよ.
(2) ヤコビアンが
を求めよ.
(2) ヤコビアンが
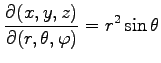 であることを用いて,多重積分
であることを用いて,多重積分 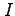 を求めよ.
を求めよ.
 |
を求める.次の問に答えよ.
(1) 座標変換
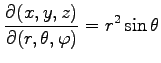 であることを用いて,多重積分
であることを用いて,多重積分
平成20年2月2日