3.21 経路に依存しない線積分
定理 3.98 (グリーンの定理の使用例)
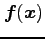 が
が  で連続でかつ
で連続でかつ 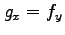 のとき,
のとき,
が成り立つ.
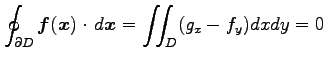 |
が成り立つ.
例 3.99 (グリーンの定理の使用例)
任意の周回積分路 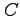 に対して,
に対して,
が成り立つ.
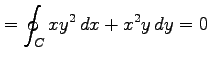 |
||
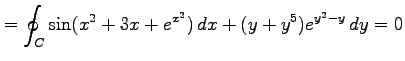 |
が成り立つ.
注意 3.100 (経路によらない線積分)
任意の周回積分路 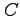 に対して,
に対して,
のとき, 点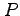 から点
から点 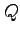 への任意の積分路
への任意の積分路 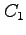 に対する線積分は
一定となる.
なぜなら,2 つの異なる点
に対する線積分は
一定となる.
なぜなら,2 つの異なる点 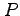 から点
から点 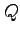 への積分路を
への積分路を
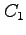 ,
, 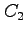 とする.
このとき
とする.
このとき 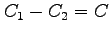 は周回する積分路となる.
よって
は周回する積分路となる.
よって
より,
を得る.
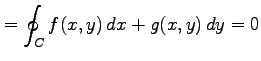 |
のとき, 点
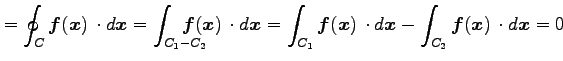 |
より,
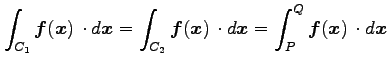 |
を得る.
例 3.101 (経路に依存しない線積分)
任意の周回積分路に関して,
が成り立つ. よって,任意の点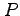 ,
, 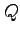 に対して
線積分
に対して
線積分
は積分の経路に依存しない. 例えば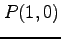 ,
, 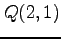 とする.
とする.
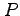 から
から 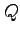 を直線的に進む経路を
を直線的に進む経路を
とする.このとき線積分は
となる. また,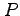 から点
から点 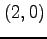 を経由し
を経由し 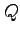 へ進む経路を
へ進む経路を
とする.このとき線積分は
となる. 異なる積分路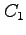 ,
, 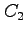 に対して積分の値は等しい.
他の経路に対しても同じ値をもつので,
に対して積分の値は等しい.
他の経路に対しても同じ値をもつので,
と書ける.
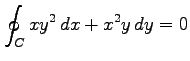 |
が成り立つ. よって,任意の点
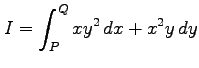 |
は積分の経路に依存しない. 例えば
とする.このとき線積分は
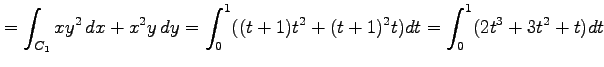 |
||
![$\displaystyle = \left[\vrule height1.5em width0em depth0.1em\,{\frac{t^4}{2}+t^3+\frac{t^2}{2}}\,\right]_0^1=2$](img2170.png) |
となる. また,
とする.このとき線積分は
![$\displaystyle =\int_{C_2}xy^2\,dx+x^2y\,dy= \int_{0}^{1}(0+0)dt+ \int_{0}^{1}(0...
...{1}4t\,dt = \left[\vrule height1.5em width0em depth0.1em\,{2t^2}\,\right]_0^1=2$](img2171.png) |
となる. 異なる積分路
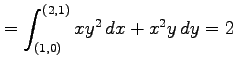 |
と書ける.
平成20年2月2日