3.22 線積分による面積の計算
注意 3.102 (線積分による面積の計算)
領域  とのその周回
とのその周回
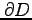 に対して
周回積分
に対して
周回積分
を考える.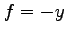 ,
, 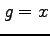 は
は
 全体で連続であるから,
領域
全体で連続であるから,
領域
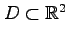 でも連続であり,
グリーンの定理が適用可能である.
よって
でも連続であり,
グリーンの定理が適用可能である.
よって
が成り立つ. よって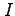 は領域
は領域  の面積
の面積 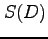 の 2 倍となる.
の 2 倍となる.
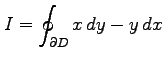 |
を考える.
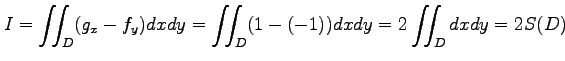 |
が成り立つ. よって
例 3.103 (線積分による面積の計算)
領域
の面積を求める. 面積は
と表される.ただし,境界線は
である.線積分を計算すると
となる.よって面積は
と求まる.![\includegraphics[width=0.4\textwidth]{sensekibun-menseki-D1.eps}](img2187.png)
の面積を求める. 面積は
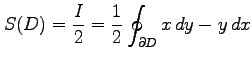 |
と表される.ただし,境界線は
である.線積分を計算すると
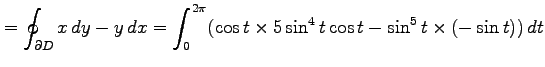 |
||
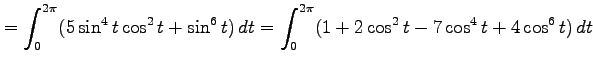 |
||
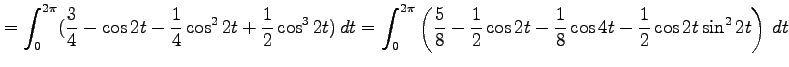 |
||
![$\displaystyle = \left[\vrule height1.5em width0em depth0.1em\,{\frac{5t}{8} -\f...
...-\frac{\sin 4t}{32} -\frac{\sin^3 2t}{12} }\,\right]_{0}^{2\pi} =\frac{5\pi}{4}$](img2185.png) |
となる.よって面積は
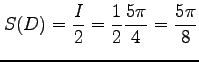 |
と求まる.
![\includegraphics[width=0.4\textwidth]{sensekibun-menseki-D1.eps}](img2187.png)
平成20年2月2日