2.1 2 変数関数
定義 2.1 (2 変数関数)
変数 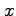 ,
, 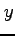 の値に対応して変数
の値に対応して変数 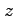 の値が定まるとき,
の値が定まるとき,
と表記し,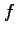 を2 変数関数という.
このとき
を2 変数関数という.
このとき 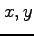 を独立変数(independent variable),
を独立変数(independent variable),
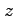 を従属変数(dependent variable)という.
を従属変数(dependent variable)という.
と表記し,
例 2.2 (2 変数関数の具体例)
関数 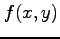 が
が
と与えられるとき,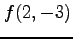 と表記するときは
と表記するときは
を意味する.
と与えられるとき,
を意味する.
問 2.3 (2 変数関数)
関数
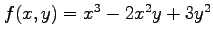 に対して,
値
に対して,
値 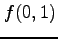 ,
, 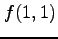 ,
, 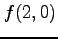 ,
, 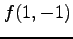 を求めよ.
を求めよ.
定義 2.4 (定義域)
関数 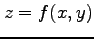 の
独立変数の組
の
独立変数の組 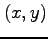 がとりうる領域を定義域(domain)という.
定義域
がとりうる領域を定義域(domain)という.
定義域  は
は 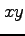 平面上の集合である.
境界を含む場合を閉領域(closed domain)と呼び,
境界を含まない場合を開領域(open domain)と呼ぶ.
平面上の集合である.
境界を含む場合を閉領域(closed domain)と呼び,
境界を含まない場合を開領域(open domain)と呼ぶ.
例 2.5 (定義域の具体例)
境界を含む長方形領域
は閉領域である. 境界を含まない長方形領域
は開領域である.
は閉領域である. 境界を含まない長方形領域
は開領域である.
例 2.6 (定義域の具体例)
原点を中心とする半径 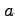 の円の境界とその内部の領域
の円の境界とその内部の領域
は閉領域である. 原点を中心とする半径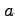 の円の内部の領域
の円の内部の領域
は開領域である.
は閉領域である. 原点を中心とする半径
は開領域である.
例 2.7 (実平面)
実 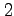 次元平面
次元平面
は開領域である.
は開領域である.
注意 2.8 (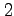 変数関数のグラフ)
定義域
変数関数のグラフ)
定義域  は
は
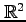 平面内の集合である.
一方,
平面内の集合である.
一方,
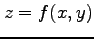 をみたす点
をみたす点 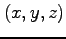 の集合は
の集合は
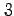 次元空間
次元空間
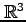 内の曲面を表す.
この曲面を関数
内の曲面を表す.
この曲面を関数 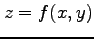 のグラフという.
のグラフという.
平成20年2月2日