1.8
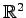 における直線の方程式
における直線の方程式
注意 1.35 (
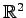 の直線の方程式)
直線
の直線の方程式)
直線
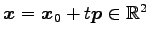 を考える.
このとき
を考える.
このとき
とおく.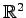 の直線の方程式は
の直線の方程式は
と表される. この式は 点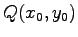 を通り
方向ベクトルが
を通り
方向ベクトルが
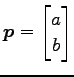 であることが
分かり易い形である.
であることが
分かり易い形である.
であり,または
となる. この式は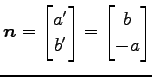 を用いると
を用いると
とも表される.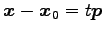 であるから,
ベクトル
であるから,
ベクトル 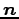 は
は
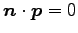 を満たす.
すなわち
を満たす.
すなわち 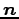 は方向ベクトル
は方向ベクトル 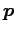 と直交する.
方向ベクトルと直交するベクトルを
法線ベクトル(normal vector)という.
と直交する.
方向ベクトルと直交するベクトルを
法線ベクトル(normal vector)という.
と表される. この式は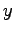 は
は 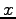 についての
についての 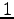 次関数であることと,
直線は点
次関数であることと,
直線は点
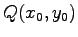 を通り
傾きが
を通り
傾きが 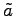 であることが分かり易い形である.
であることが分かり易い形である.
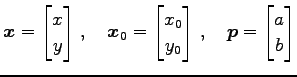 |
(38) |
とおく.
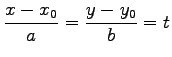 |
(39) |
と表される. この式は 点
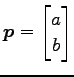 であることが
分かり易い形である.
であることが
分かり易い形である.
式変形をする.
![]() ,
, ![]() ,
,
![]() とおく.
すると
とおく.
すると
| (40) |
であり,または
| (41) |
となる. この式は
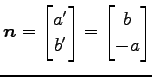 を用いると
を用いると
| (42) |
とも表される.
さらに式変形する.
![]() とおく.
すると
とおく.
すると
| (43) |
と表される. この式は
注意 1.36 (
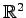 の直線の方程式)
の直線の方程式)
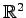 の直線の方程式はいくつかの書き方がある.
まず,
の直線の方程式はいくつかの書き方がある.
まず,
と書くとき,![$ \begin{bmatrix}{a}\\ [-.5ex]{b}\end{bmatrix}$](img195.png) は
方向ベクトルを表す.
は
方向ベクトルを表す.
と書くときでは,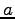 は傾きを
は傾きを 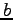 は
は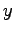 切片をそれぞれ表す.
切片をそれぞれ表す.
と書くときは,![$ \begin{bmatrix}{a}\\ [-.5ex]{b}\end{bmatrix}$](img195.png) は
法線ベクトルを表す.
は
法線ベクトルを表す.
と書けば,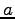 は
は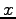 切片を
切片を 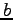 は
は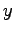 切片をそれぞれ表す.
切片をそれぞれ表す.
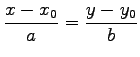 |
(44) |
と書くとき,
| (45) |
と書くときでは,
| (46) |
と書くときは,
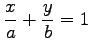 |
(47) |
と書けば,
例 1.37 (
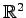 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 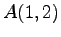 ,
, 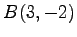 を通る直線の方程式を考える.
まず
を通る直線の方程式を考える.
まず
とおく.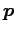 は方向ベクトルである.
直線の方程式のパラメータ表示は
は方向ベクトルである.
直線の方程式のパラメータ表示は
である.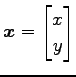 とおき
とおき  を消去すると,
直線の方程式の成分表示は
を消去すると,
直線の方程式の成分表示は
であり,変形して
である.法線ベクトルは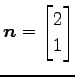 である.
さらに変形して
である.
さらに変形して
となる.傾きは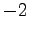 であり,
であり,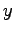 切片は
切片は 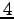 である.
さらに変形して
である.
さらに変形して
となる.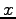 切片は
切片は 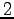 であり,
であり,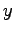 切片は
切片は 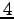 である.
である.
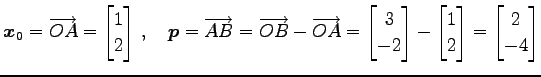 |
(48) |
とおく.
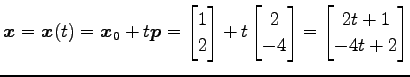 |
(49) |
である.
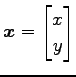 とおき
とおき 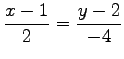 |
(50) |
であり,変形して
| (51) |
である.法線ベクトルは
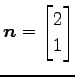 である.
さらに変形して
である.
さらに変形して
| (52) |
となる.傾きは
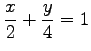 |
(53) |
となる.
例 1.38 (
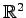 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 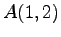 ,
, 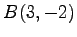 を通る直線の方程式を考える.
直線の方程式を
を通る直線の方程式を考える.
直線の方程式を
と仮定する. 点 ,
, 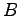 は直線上にあるので
は直線上にあるので
が成り立つ. この連立方程式を解くと
となる.直線の方程式を
と得る.
| (54) |
と仮定する. 点
| (55) |
が成り立つ. この連立方程式を解くと
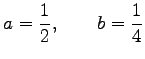 |
(56) |
となる.直線の方程式を
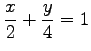 |
(57) |
と得る.
注意 1.39 (
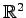 の直線の方程式)
直線は
の直線の方程式)
直線は 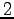 点より定まることと
連立方程式の解が一意に定まることとは等価である.
点より定まることと
連立方程式の解が一意に定まることとは等価である.
例 1.40 (直線)
2 点 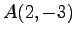 ,
, 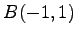 を通る直線を考える.
この直線の方向ベクトルは
を通る直線を考える.
この直線の方向ベクトルは
である.直線の方程式のパラメータ表示は
である.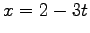 ,
, 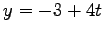 で
で  を消去すると
を消去すると
となる.式変形して
とする. この式より,この直線は法線ベクトルが
で点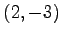 を通る直線である.
さらに式変形して一般形で表すと
を通る直線である.
さらに式変形して一般形で表すと
である. また,式変形して
とする. 直線の傾きは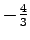 であり,
であり,
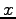 切片は
切片は
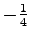 で
で
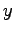 切片は
切片は
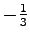 である.
である.
である.式変形すれば
と書ける. 法線は傾きが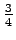 で,
で,
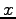 切片が
切片が 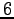 で,
で,
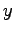 切片が
切片が
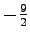 で,
法線ベクトルが
で,
法線ベクトルが
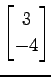 である.
である.
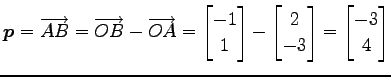 |
である.直線の方程式のパラメータ表示は
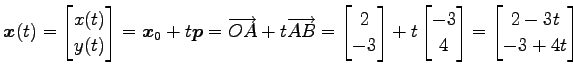 |
である.
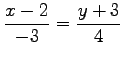 |
となる.式変形して
とする. この式より,この直線は法線ベクトルが
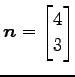 |
で点
である. また,式変形して
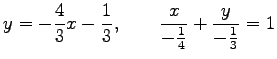 |
とする. 直線の傾きは
次にこの直線と直交し点 ![]() を通る直線を考える.
法線ベクトル
を通る直線を考える.
法線ベクトル ![]() が方向ベクトルとるので,
法線の方程式は
が方向ベクトルとるので,
法線の方程式は
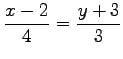 |
である.式変形すれば
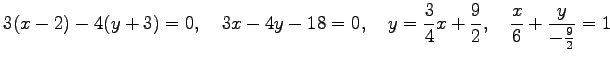 |
と書ける. 法線は傾きが
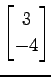 である.
である.
平成20年2月2日