1.15 内積の幾何学的イメージ
注意 1.81 (ベクトルの内積の図説)
ベクトル 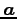 と
と 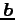 の成す角を
の成す角を 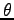 とするとき
とするとき
が成り立つ. すなわち,辺の長さが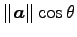 と
と
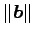 の長方形の面積を表す.
角度
の長方形の面積を表す.
角度 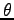 の値により面積は変化する.
の値により面積は変化する.
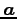 と
と 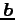 とが
同じ向きのとき,すなわち
とが
同じ向きのとき,すなわち 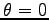 のときは,
面積は最大値をとり
のときは,
面積は最大値をとり
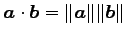 で与えられる.
で与えられる.
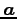 と
と 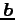 とが直交し
とが直交し
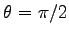 のときは,
面積は最小値をとり
のときは,
面積は最小値をとり
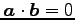 で与えられる.
で与えられる.
| (98) |
が成り立つ. すなわち,辺の長さが
平成20年2月2日