1.16 平行四辺形の面積
定理 1.82 (平行四辺形の面積)
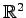 内の点
内の点 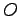 ,
,
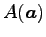 ,
,
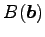 ,
,
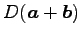 を考える.
このとき平行四辺形
を考える.
このとき平行四辺形  の面積は
の面積は
で与えられる.ただし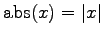 とする.
とする.
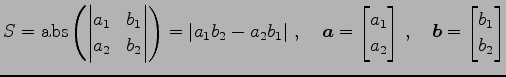 |
(99) |
で与えられる.ただし
問 1.83 (平行四辺形の面積)
これを証明せよ.
を得る.
が
を満すとする. このとき
が成り立つ.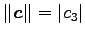 はベクトル
はベクトル 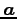 ,
, 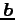 が
なす平行四辺形の面積に等しい.
が
なす平行四辺形の面積に等しい.
(証明その1)
角度
![]() とする.
平行四辺形の面積は底辺の長さ
とする.
平行四辺形の面積は底辺の長さ
![]() と
高さ
と
高さ
![]() を掛けたものであるので,
これを計算すると
を掛けたものであるので,
これを計算すると
| (100) | ||
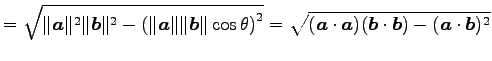 |
(101) | |
| (102) | ||
| (103) |
を得る.
(証明その2)
![]() のベクトル
のベクトル
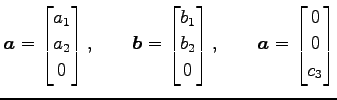 |
(104) |
が
| (105) |
を満すとする. このとき
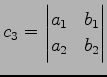 |
(106) |
が成り立つ.
平成20年2月2日