1.19 外積を成分で計算
注意 1.92 (外積の成分表示)
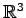 のベクトル
のベクトル 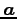 ,
, 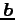 を
を  平面上とする.
すなわち,
平面上とする.
すなわち,
![$ \vec{a}=\begin{bmatrix}{a_1}\\ [-.5ex]{a_2}\\ [-.5ex]{0}\end{bmatrix}$](img467.png) ,
,
![$ \vec{b}=\begin{bmatrix}{b_1}\\ [-.5ex]{b_2}\\ [-.5ex]{0}\end{bmatrix}$](img468.png) とおく.
このとき,4 点
とおく.
このとき,4 点 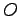 ,
,
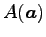 ,
,
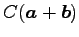 ,
,
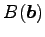 からなる平行四辺形の面積は
からなる平行四辺形の面積は
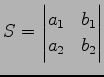 である.ここで符合は
である.ここで符合は 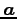 ,
, 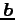 の向きに正とする.
外積
の向きに正とする.
外積
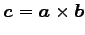 は
は 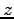 軸と同じ向きで
大きさは
軸と同じ向きで
大きさは 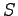 となるで,
となるで,
と得られる.
![$ \vec{a}=\begin{bmatrix}{a_1}\\ [-.5ex]{a_2}\\ [-.5ex]{0}\end{bmatrix}$](img467.png) ,
,
![$ \vec{b}=\begin{bmatrix}{b_1}\\ [-.5ex]{b_2}\\ [-.5ex]{0}\end{bmatrix}$](img468.png) とおく.
このとき,4 点
とおく.
このとき,4 点 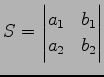 である.ここで符合は
である.ここで符合は 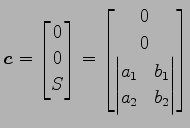 |
と得られる.
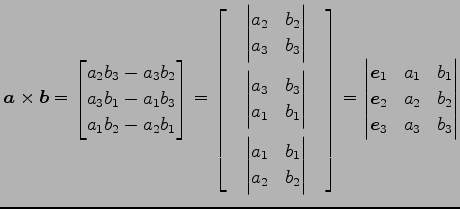
定理 1.93 (外積の成分表示)
 のベクトル
のベクトル
![$ \vec{a}=\begin{bmatrix}{a_{1}}\\ [-.5ex]{a_{2}}\\ [-.5ex]{a_{3}}\end{bmatrix}$](img472.png) ,
,
![$ \vec{b}=\begin{bmatrix}{b_{1}}\\ [-.5ex]{b_{2}}\\ [-.5ex]{b_{3}}\end{bmatrix}$](img473.png) に対して,
に対して,
が成り立つ.
![$ \vec{a}=\begin{bmatrix}{a_{1}}\\ [-.5ex]{a_{2}}\\ [-.5ex]{a_{3}}\end{bmatrix}$](img472.png) ,
,
![$ \vec{b}=\begin{bmatrix}{b_{1}}\\ [-.5ex]{b_{2}}\\ [-.5ex]{b_{3}}\end{bmatrix}$](img473.png) に対して,
に対して,
 |
(108) |
が成り立つ.
問 1.94 (外積の成分表示)
これを示せ.
例 1.95 (外積の計算例)
![$ \vec{a}=\begin{bmatrix}{1}\\ [-.5ex]{2}\\ [-.5ex]{3}\end{bmatrix}$](img475.png) ,
,
![$ \vec{b}=\begin{bmatrix}{4}\\ [-.5ex]{5}\\ [-.5ex]{6}\end{bmatrix}$](img476.png) の外積は
の外積は
である.
![$ \vec{a}=\begin{bmatrix}{1}\\ [-.5ex]{2}\\ [-.5ex]{3}\end{bmatrix}$](img475.png) ,
,
![$ \vec{b}=\begin{bmatrix}{4}\\ [-.5ex]{5}\\ [-.5ex]{6}\end{bmatrix}$](img476.png) の外積は
の外積は
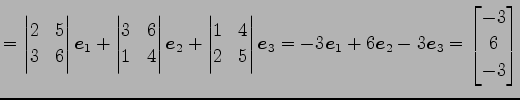 |
(109) |
である.
平成20年2月2日