1.21 スカラー三重積と平行六面体の体積
問 1.98 (スカラー三重積)
すべての
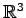 のベクトル
のベクトル 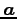 ,
, 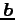 ,
, 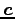 に対して
に対して
が成り立つことを示せ.
| (124) |
が成り立つことを示せ.
定義 1.99 (スカラー三重積)
スカラー三重積(scalar triple vector)を
と定義する.
| (125) |
と定義する.
定理 1.100 (スカラー三重積の値)
![$\displaystyle [\vec{a},\vec{b},\vec{c}]= \begin{vmatrix}a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{vmatrix}$](img498.png) |
(126) |
問 1.101 (スカラー三重積の値)
これを示せ.
(証明)
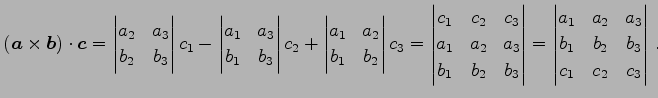 |
(127) |
問 1.102 (外積の性質)
次の関係式を示せ.
(1)![$ (\vec{a}\times\vec{b})\times(\vec{c}\times\vec{d})=
[\vec{a},\vec{b},\vec{d}]\vec{c}-
[\vec{a},\vec{b},\vec{c}]\vec{d}$](img500.png)
(2)![$ [\vec{a}\times\vec{b},\vec{b}\times\vec{c},\vec{c}\times\vec{a}]=
[\vec{a},\vec{b},\vec{c}]^2$](img501.png)
(3)![$ [\vec{a}\times\vec{b},\vec{c}\times\vec{d},\vec{e}\times\vec{f}]=
[\vec{a},\ve...
...}][\vec{c},\vec{e},\vec{f}]-
[\vec{a},\vec{b},\vec{c}][\vec{d},\vec{e},\vec{f}]$](img502.png)
(4)![$ \displaystyle{
[\vec{a},\vec{b},\vec{c}][\vec{l},\vec{m},\vec{n}]=
\begin{vmat...
...
\vec{c}\cdot\vec{l} &
\vec{c}\cdot\vec{m} &
\vec{c}\cdot\vec{n}
\end{vmatrix}}$](img503.png)
(1)
(2)
(3)
(4)
![$ \displaystyle{
[\vec{a},\vec{b},\vec{c}][\vec{l},\vec{m},\vec{n}]=
\begin{vmat...
...
\vec{c}\cdot\vec{l} &
\vec{c}\cdot\vec{m} &
\vec{c}\cdot\vec{n}
\end{vmatrix}}$](img503.png)
問 1.103 (スカラー三重積と体積)
頂点が 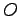 ,
,
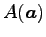 ,
,
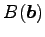 ,
,
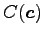 ,
,
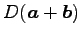 ,
,
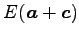 ,
,
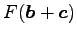 ,
,
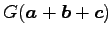 である並行 6 面体の体積は
である並行 6 面体の体積は
![$ V=\left\vert[\vec{a},\vec{b},\vec{c}]\right\vert$](img507.png) である.
これを示せ.
である.
これを示せ.
(答え)
平行 6 面体の体積は,
底面積を ![]() とし,
高さを
とし,
高さを ![]() とすると,
とすると,
![]() で与えれる.
底面の平行四辺形
で与えれる.
底面の平行四辺形 ![]() の面積は,
の面積は,
![]() である.
また,底面に対する単位法線ベクトルは
である.
また,底面に対する単位法線ベクトルは
![]() である.
ベクトル
である.
ベクトル ![]() を垂線に正射影してできるベクトルの長さが
高さ
を垂線に正射影してできるベクトルの長さが
高さ ![]() であるから,
であるから,
![]() となる.
よって体積は
となる.
よって体積は
![]() と求まる.
と求まる.
![\includegraphics[width=0.9\textwidth]{V6.eps}](img515.png)
平成20年2月2日