1.22 演習問題 〜 内積,ノルム,外積
問 1.104 (内積,ノルム,外積)
 のベクトルに対して,
次の関係式が成り立つこと証明せよ.
のベクトルに対して,
次の関係式が成り立つこと証明せよ.
(1)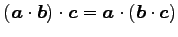 (2)
(2)
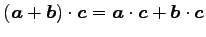 (3)
(3)
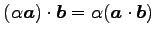 (4)
(4)
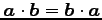
(5)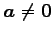 のとき
のとき
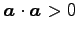 (6)
(6)
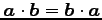 (7)
(7)
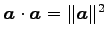 (8)
(8)
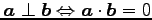
(9)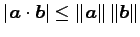 (10)
(10)
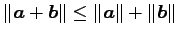 (11)
(11)
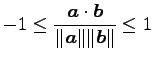
(12)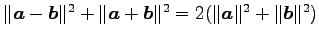 (13)
(13)
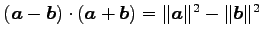
(14)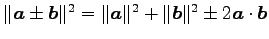 (15)
(15)
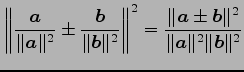
(16)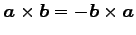 (17)
(17)
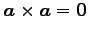 (18)
(18)
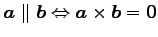 (19)
(19)
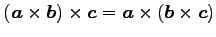
(20)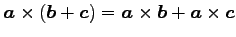 (21)
(21)
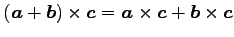
(22)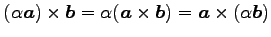 (23)
(23)
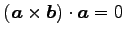 (24)
(24)
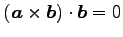
(25)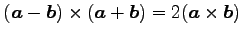 (26)
(26)
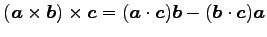
(27)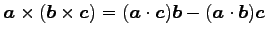 (28)
(28)
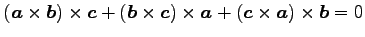
(29)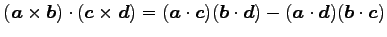 (30)
(30)
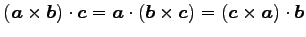
(31)![$ \displaystyle{
\vec{a}\cdot(\vec{b}\times(\vec{c}\times\vec{d}))=
(\vec{a}\tim...
...cdot\vec{c} \\ [-.3ex]
\vec{a}\cdot\vec{d} &
\vec{b}\cdot\vec{d}
\end{vmatrix}}$](img465.png)
(32)![$ (\vec{a}\times\vec{b})\times(\vec{c}\times\vec{d})=
[\vec{a},\vec{b},\vec{d}]\vec{c}-
[\vec{a},\vec{b},\vec{c}]\vec{d}$](img500.png) (33)
(33)
![$ [\vec{a}\times\vec{b},\vec{b}\times\vec{c},\vec{c}\times\vec{a}]=
[\vec{a},\vec{b},\vec{c}]^2$](img501.png)
(34)![$ [\vec{a}\times\vec{b},\vec{c}\times\vec{d},\vec{e}\times\vec{f}]=
[\vec{a},\ve...
...}][\vec{c},\vec{e},\vec{f}]-
[\vec{a},\vec{b},\vec{c}][\vec{d},\vec{e},\vec{f}]$](img502.png)
(35)![$ \displaystyle{
[\vec{a},\vec{b},\vec{c}][\vec{l},\vec{m},\vec{n}]=
\begin{vmat...
...
\vec{c}\cdot\vec{l} &
\vec{c}\cdot\vec{m} &
\vec{c}\cdot\vec{n}
\end{vmatrix}}$](img503.png)
(1)
(5)
(9)
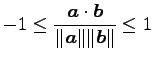
(12)
(14)
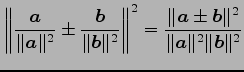
(16)
(20)
(22)
(25)
(27)
(29)
(31)
![$ \displaystyle{
\vec{a}\cdot(\vec{b}\times(\vec{c}\times\vec{d}))=
(\vec{a}\tim...
...cdot\vec{c} \\ [-.3ex]
\vec{a}\cdot\vec{d} &
\vec{b}\cdot\vec{d}
\end{vmatrix}}$](img465.png)
(32)
(34)
(35)
![$ \displaystyle{
[\vec{a},\vec{b},\vec{c}][\vec{l},\vec{m},\vec{n}]=
\begin{vmat...
...
\vec{c}\cdot\vec{l} &
\vec{c}\cdot\vec{m} &
\vec{c}\cdot\vec{n}
\end{vmatrix}}$](img503.png)
問 1.105 (内積)
次の 2 つのベクトルのノルムをそれぞれ求めよ.またこれらの内積,方向余弦,成す角を求めよ.
(1)![$ \begin{bmatrix}{-\sqrt{3}}\\ [-.5ex]{1}\end{bmatrix}$](img521.png) ,
,
![$ \begin{bmatrix}{3}\\ [-.5ex]{\sqrt{3}}\end{bmatrix}$](img522.png) (2)
(2)
![$ \begin{bmatrix}{1}\\ [-.5ex]{2}\end{bmatrix}$](img523.png) ,
,
![$ \begin{bmatrix}{-2}\\ [-.5ex]{3}\end{bmatrix}$](img524.png) (3)
(3)
![$ \begin{bmatrix}{1}\\ [-.5ex]{2}\\ [-.5ex]{1}\end{bmatrix}$](img525.png) ,
,
![$ \begin{bmatrix}{-2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}$](img526.png) (4)
(4)
![$ \begin{bmatrix}{0}\\ [-.5ex]{1}\\ [-.5ex]{-1}\end{bmatrix}$](img527.png) ,
,
![$ \begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{-2}\end{bmatrix}$](img528.png)
(5)![$ \begin{bmatrix}{1}\\ [-.5ex]{-1}\\ [-.5ex]{0}\\ [-.5ex]{2}\end{bmatrix}$](img529.png) ,
,
![$ \begin{bmatrix}{2}\\ [-.5ex]{1}\\ [-.5ex]{3}\\ [-.5ex]{0}\end{bmatrix}$](img530.png) (6)
(6)
![$ \begin{bmatrix}{-1}\\ [-.5ex]{2}\\ [-.5ex]{3}\\ [-.5ex]{0}\\ [-.5ex]{1}\end{bmatrix}$](img531.png) ,
,
![$ \begin{bmatrix}{1}\\ [-.5ex]{-1}\\ [-.5ex]{2}\\ [-.5ex]{1}\\ [-.5ex]{-1}\end{bmatrix}$](img532.png)
(1)
![$ \begin{bmatrix}{-\sqrt{3}}\\ [-.5ex]{1}\end{bmatrix}$](img521.png) ,
,
![$ \begin{bmatrix}{3}\\ [-.5ex]{\sqrt{3}}\end{bmatrix}$](img522.png) (2)
(2)
![$ \begin{bmatrix}{-2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}$](img526.png) (4)
(4)
![$ \begin{bmatrix}{0}\\ [-.5ex]{1}\\ [-.5ex]{-1}\end{bmatrix}$](img527.png) ,
,
![$ \begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{-2}\end{bmatrix}$](img528.png)
(5)
![$ \begin{bmatrix}{1}\\ [-.5ex]{-1}\\ [-.5ex]{0}\\ [-.5ex]{2}\end{bmatrix}$](img529.png) ,
,
![$ \begin{bmatrix}{-1}\\ [-.5ex]{2}\\ [-.5ex]{3}\\ [-.5ex]{0}\\ [-.5ex]{1}\end{bmatrix}$](img531.png) ,
,
![$ \begin{bmatrix}{1}\\ [-.5ex]{-1}\\ [-.5ex]{2}\\ [-.5ex]{1}\\ [-.5ex]{-1}\end{bmatrix}$](img532.png)
問 1.106 (内積)
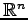 のベクトル
のベクトル  ,
, 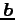 が
が
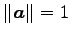 ,
,
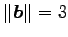 ,
,
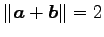 をみたすとき,
をみたすとき,
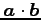 と
と
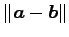 の値を求めよ.
の値を求めよ.
問 1.107 (内積)
 のベクトル
のベクトル
![$ \vec{a}=\begin{bmatrix}{1}\\ [-.5ex]{2}\end{bmatrix}$](img538.png) ,
,
![$ \vec{b}=\begin{bmatrix}{3}\\ [-.5ex]{8}\end{bmatrix}$](img539.png) ,
,
![$ \vec{c}=\begin{bmatrix}{1}\\ [-.5ex]{-1}\end{bmatrix}$](img540.png) が
が
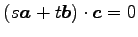 をみたすような実数
をみたすような実数
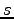 ,
,  を求めよ.
ただし
を求めよ.
ただし 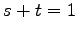 とする.
このとき
とする.
このとき
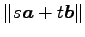 の値を求めよ.
の値を求めよ.
![$ \vec{a}=\begin{bmatrix}{1}\\ [-.5ex]{2}\end{bmatrix}$](img538.png) ,
,
![$ \vec{b}=\begin{bmatrix}{3}\\ [-.5ex]{8}\end{bmatrix}$](img539.png) ,
,
![$ \vec{c}=\begin{bmatrix}{1}\\ [-.5ex]{-1}\end{bmatrix}$](img540.png) が
が
問 1.108 (方向余弦)
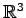 の
の 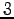 点
点 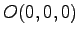 ,
, 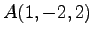 ,
, 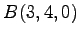 に対して,
方向余弦
に対して,
方向余弦
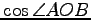 を求めよ.
また,
を求めよ.
また,
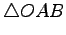 の面積を求めよ.
の面積を求めよ.
問 1.109 (直交)
次のベクトルに直交するベクトルを 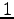 つ求めよ.
つ求めよ.
(1)![$ \begin{bmatrix}{2}\\ [-.5ex]{-1}\end{bmatrix}$](img550.png) (2)
(2)
![$ \begin{bmatrix}{1}\\ [-.5ex]{1}\\ [-.5ex]{0}\end{bmatrix}$](img551.png) ,
,
![$ \begin{bmatrix}{0}\\ [-.5ex]{1}\\ [-.5ex]{1}\end{bmatrix}$](img552.png) (3)
(3)
![$ \begin{bmatrix}{1}\\ [-.5ex]{-2}\\ [-.5ex]{3}\end{bmatrix}$](img553.png) (4)
(4)
![$ \begin{bmatrix}{-1}\\ [-.5ex]{2}\\ [-.5ex]{1}\\ [-.5ex]{-1}\end{bmatrix}$](img554.png) (5)
(5)
![$ \begin{bmatrix}{2}\\ [-.5ex]{0}\\ [-.5ex]{-1}\\ [-.5ex]{1}\\ [-.5ex]{3}\end{bmatrix}$](img555.png)
(1)
![$ \begin{bmatrix}{1}\\ [-.5ex]{-2}\\ [-.5ex]{3}\end{bmatrix}$](img553.png) (4)
(4)
![$ \begin{bmatrix}{-1}\\ [-.5ex]{2}\\ [-.5ex]{1}\\ [-.5ex]{-1}\end{bmatrix}$](img554.png) (5)
(5)
![$ \begin{bmatrix}{2}\\ [-.5ex]{0}\\ [-.5ex]{-1}\\ [-.5ex]{1}\\ [-.5ex]{3}\end{bmatrix}$](img555.png)
問 1.110 (外積)
次のベクトルの外積を求めよ.
(1)![$ \begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}\times\begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{1}\end{bmatrix}$](img556.png) (2)
(2)
![$ \begin{bmatrix}{1}\\ [-.5ex]{2}\\ [-.5ex]{-1}\end{bmatrix}\times\begin{bmatrix}{3}\\ [-.5ex]{2}\\ [-.5ex]{-1}\end{bmatrix}$](img557.png) (3)
(3)
![$ \begin{bmatrix}{0}\\ [-.5ex]{1}\\ [-.5ex]{2}\end{bmatrix}\times\begin{bmatrix}{-1}\\ [-.5ex]{-1}\\ [-.5ex]{2}\end{bmatrix}$](img558.png)
(1)
![$ \begin{bmatrix}{2}\\ [-.5ex]{-1}\\ [-.5ex]{1}\end{bmatrix}\times\begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{1}\end{bmatrix}$](img556.png) (2)
(2)
![$ \begin{bmatrix}{1}\\ [-.5ex]{2}\\ [-.5ex]{-1}\end{bmatrix}\times\begin{bmatrix}{3}\\ [-.5ex]{2}\\ [-.5ex]{-1}\end{bmatrix}$](img557.png) (3)
(3)
![$ \begin{bmatrix}{0}\\ [-.5ex]{1}\\ [-.5ex]{2}\end{bmatrix}\times\begin{bmatrix}{-1}\\ [-.5ex]{-1}\\ [-.5ex]{2}\end{bmatrix}$](img558.png)
問 1.111 (外積)
次の外積を計算せよ.
(1)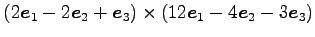 (2)
(2)
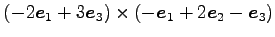
(3)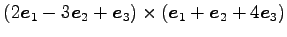
ただし, の基本ベクトルを
の基本ベクトルを
![$ \vec{e}_1=\begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{0}\end{bmatrix}$](img562.png) ,
,
![$ \vec{e}_2=\begin{bmatrix}{0}\\ [-.5ex]{1}\\ [-.5ex]{0}\end{bmatrix}$](img563.png) ,
,
![$ \vec{e}_3=\begin{bmatrix}{0}\\ [-.5ex]{0}\\ [-.5ex]{1}\end{bmatrix}$](img564.png) とする.
とする.
(1)
(3)
ただし,
![$ \vec{e}_1=\begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{0}\end{bmatrix}$](img562.png) ,
,
![$ \vec{e}_2=\begin{bmatrix}{0}\\ [-.5ex]{1}\\ [-.5ex]{0}\end{bmatrix}$](img563.png) ,
,
![$ \vec{e}_3=\begin{bmatrix}{0}\\ [-.5ex]{0}\\ [-.5ex]{1}\end{bmatrix}$](img564.png) とする.
とする.
問 1.112 (外積)
ベクトル
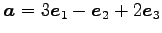 ,
,
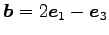 ,
,
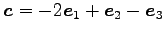 に対して次を求めよ.
に対して次を求めよ.
(1)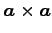 (2)
(2)
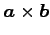 (3)
(3)
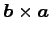 (4)
(4)
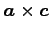 (5)
(5)
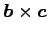 (6)
(6)
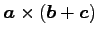 (7)
(7)
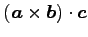
(8)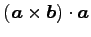 (9)
(9)
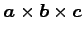 (10)
(10)
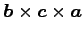 (11)
(11)
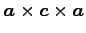
(1)
(8)
問 1.113 (右手系)
ベクトル 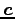 はベクトル
はベクトル 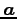 ,
, 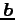 に垂直なベクトルであり,
かつ
に垂直なベクトルであり,
かつ 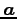 ,
, 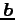 ,
, 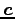 はこの順序で右手系をなすとする.
はこの順序で右手系をなすとする.
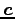 を求めよ.
を求めよ.
(1)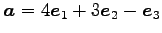 ,
,
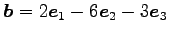 (2)
(2)
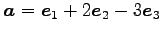 ,
,
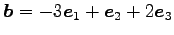
(3)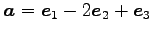 ,
,
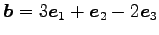
(1)
(3)
問 1.114 (右手系)
ベクトル 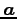 ,
, 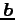 ,
, 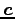 は
この順で右手系であり,お互いに直交するとする.
は
この順で右手系であり,お互いに直交するとする.
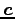 を求めよ.
を求めよ.
(1)![$ \vec{a}=\begin{bmatrix}{-1}\\ [-.5ex]{-1}\\ [-.5ex]{2}\end{bmatrix}$](img584.png) ,
,
![$ \vec{b}=\begin{bmatrix}{3}\\ [-.5ex]{1}\\ [-.5ex]{2}\end{bmatrix}$](img585.png) (2)
(2)
![$ \vec{a}=\begin{bmatrix}{-1}\\ [-.5ex]{2}\\ [-.5ex]{-1}\end{bmatrix}$](img586.png) ,
,
![$ \vec{b}=\begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{-1}\end{bmatrix}$](img587.png) (3)
(3)
![$ \vec{a}=\begin{bmatrix}{2}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}$](img588.png) ,
,
![$ \vec{b}=\begin{bmatrix}{-1}\\ [-.5ex]{1}\\ [-.5ex]{1}\end{bmatrix}$](img589.png)
(1)
![$ \vec{a}=\begin{bmatrix}{-1}\\ [-.5ex]{-1}\\ [-.5ex]{2}\end{bmatrix}$](img584.png) ,
,
![$ \vec{b}=\begin{bmatrix}{3}\\ [-.5ex]{1}\\ [-.5ex]{2}\end{bmatrix}$](img585.png) (2)
(2)
![$ \vec{a}=\begin{bmatrix}{-1}\\ [-.5ex]{2}\\ [-.5ex]{-1}\end{bmatrix}$](img586.png) ,
,
![$ \vec{b}=\begin{bmatrix}{1}\\ [-.5ex]{0}\\ [-.5ex]{-1}\end{bmatrix}$](img587.png) (3)
(3)
![$ \vec{a}=\begin{bmatrix}{2}\\ [-.5ex]{3}\\ [-.5ex]{-1}\end{bmatrix}$](img588.png) ,
,
![$ \vec{b}=\begin{bmatrix}{-1}\\ [-.5ex]{1}\\ [-.5ex]{1}\end{bmatrix}$](img589.png)
問 1.115 (平行四辺形の面積)
次の
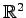 の 4 点からなる平行四辺形の面積を求めよ.
の 4 点からなる平行四辺形の面積を求めよ.
(1)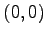 ,
, 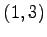 ,
, 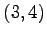 ,
, 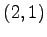 (2)
(2) 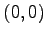 ,
, 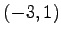 ,
, 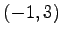 ,
, 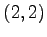
(3)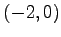 ,
, 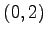 ,
, 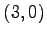 ,
, 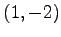
(1)
(3)
問 1.116 (平行四辺形の面積)
次の
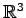 の 4 点からなる平行四辺形の面積を求めよ.
の 4 点からなる平行四辺形の面積を求めよ.
(1)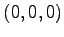 ,
, 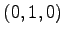 ,
, 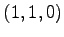 ,
, 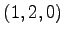 (2)
(2) 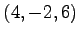 ,
, 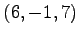 ,
, 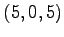 ,
, 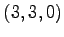
(3)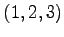 ,
, 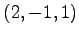 ,
, 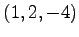 ,
, 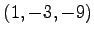
(1)
(3)
問 1.117 (平行六面体の体積)
次の
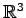 の 8 点からなる平行六面体の体積を求めよ.
の 8 点からなる平行六面体の体積を求めよ.
(1)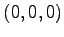 ,
, 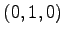 ,
, 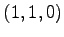 ,
, 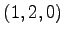 ,
,
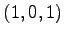 ,
, 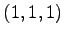 ,
, 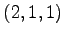 ,
, 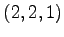
(2)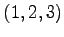 ,
, 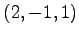 ,
, 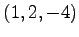 ,
, 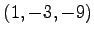 ,
,
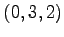 ,
, 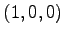 ,
, 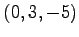 ,
,
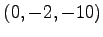
(1)
(2)
平成20年2月2日